题目内容
8.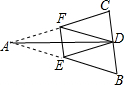 如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )
如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )| A. | 2$\sqrt{10}$ | B. | 4$\sqrt{10}$ | C. | 12 | D. | 24 |
分析 首先在RT△ABD中,证明ED=EA=EB,并且求出线段AD,同理可以证明AF=FC,根据三角形中位线定理求出BC,根据勾股定理求出AD,由此即可解决问题.
解答 解:∵AB=AC,BD=CD,
∴AD⊥BC,∠ADB=90°,
∵△EFD是由△AEF翻折,
∴AE=ED,
∴∠EAD=∠EDA,
∵∠EAD+∠B=90°,∠EDA+∠EDB=90°,
∴∠B=∠EDB,
∴ED=EB=AE,同理DF=AF=FC,
∴EF=$\frac{1}{2}$BC,
∵DE=$\sqrt{10}$,EF=2,
∴BC=4,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{(2\sqrt{10})^{2}-{2}^{2}}$=6,
∴${S}_{△ABC}=\frac{1}{2}•BC•AD$=$\frac{1}{2}$×4×6=12.
故选C.
点评 本题考查翻折变换、三角形中位线定理,勾股定理等知识,解决问题的关键是求出底和高利用三角形面积公式计算,属于中考常考题型.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.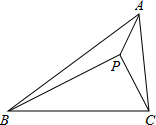 如图,△ABC中,∠BAC=60°,AB=2AC,点P在△ABC内,且PA=$\sqrt{3}$,PB=5,PC=2,则△ABC的面积为( )
如图,△ABC中,∠BAC=60°,AB=2AC,点P在△ABC内,且PA=$\sqrt{3}$,PB=5,PC=2,则△ABC的面积为( )
 如图,△ABC中,∠BAC=60°,AB=2AC,点P在△ABC内,且PA=$\sqrt{3}$,PB=5,PC=2,则△ABC的面积为( )
如图,△ABC中,∠BAC=60°,AB=2AC,点P在△ABC内,且PA=$\sqrt{3}$,PB=5,PC=2,则△ABC的面积为( )| A. | 3+$\frac{7}{2}$$\sqrt{3}$ | B. | 3+$\frac{5}{2}$$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\frac{1}{2}$$\sqrt{3}$ |
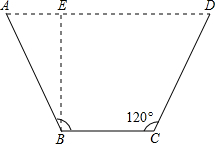 用一块宽度为5m的长方形铁片弯折成如图所示的梯形流水槽,其中BC∥AD,AB=DC,要使流水的截面面积最大,弯折的长度(AB的长)应是多少?
用一块宽度为5m的长方形铁片弯折成如图所示的梯形流水槽,其中BC∥AD,AB=DC,要使流水的截面面积最大,弯折的长度(AB的长)应是多少?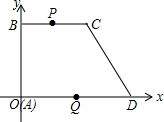 如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0).点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(一点到达,另一点也停止运动).
如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0).点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(一点到达,另一点也停止运动).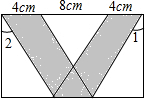 如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.
如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.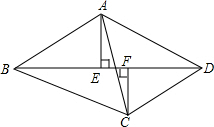 如图,在四边形ABCD中,AE⊥BD,CF⊥BD,且AE=CF,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AE⊥BD,CF⊥BD,且AE=CF,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.