题目内容
6.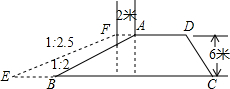 如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.(1)求加宽部分横截面的面积.
(2)完成这一工程需要多少立方米的土?
分析 (1)首先过点A作AG⊥BC,过点F作FH⊥BC,垂足分别是G、H.易得FH=AG=6米.HG=AF=2米,然后由坡度由原来的1:2改成1:2.5,求得BG与EH的长,继而求得加宽部分横断面AFEB的面积;
(2)根据坝长50米,即可求得完成这一工程需要多少方土.
解答  解:(1)过点A作AG⊥BC,过点F作FH⊥BC,垂足分别是G、H.
解:(1)过点A作AG⊥BC,过点F作FH⊥BC,垂足分别是G、H.
根据题意得:FH=AG=6米.HG=AF=2米,
在Rt△AGB和Rt△FHE中,
∵tan∠ABG=$\frac{AG}{BG}$=$\frac{1}{2}$,tan∠E=$\frac{FH}{EH}$=$\frac{1}{2.5}$,
∴BG=2AG,EH=2.5FH,
则BG=12(米),EH=15(米),
∴EB=EH-BH=15-(12-2)=5(米),
∴S梯形AFEB=$\frac{1}{2}$(AF+EB)•FH=$\frac{1}{2}$×(2+5)×6=21(米2),
答:加宽部分横断面AFEB的面积为21平方米;
(2)完成这一项工程需要的土方:V=21×50=1050(米3),
答:完成这一工程需要1050立方米的土.
点评 此题考查了坡度坡角问题.此题难度适中,注意构造直角三角形,并解直角三角形是解此题的关键.

练习册系列答案
相关题目
16.在离古塔a米的P点,用测角仪测得塔顶的仰角为α,已知测角仪的高度为h米,那么塔高为( )
| A. | atanα+h | B. | acotα+h | C. | $\sqrt{{a}^{2}+{h}^{2}}$ | D. | (a+h)•cosα |
17.已知点(a+1,y1),(a-2,y2)都在函数y=x2-2ax+b的图象上,则( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不确定 |
14.某项工程甲单独做6天完成,乙单独做8天完成,若甲先干一天,然后甲、乙合作完成此项工一共做了x天,则所列方程为( )
| A. | $\frac{x+1}{6}$+$\frac{x}{8}$=1 | B. | $\frac{x}{6}$+$\frac{x+1}{8}$=1 | C. | $\frac{x}{6}$+$\frac{x-1}{8}$=1 | D. | $\frac{x}{6}$+$\frac{1}{6}$+$\frac{x-1}{8}$=1 |
18.下列命题中.正确的是( )
| A. | 若a>0,则$\sqrt{{a}^{2}}$=a | B. | 若$\sqrt{{a}^{2}}$=a,则a>0 | ||
| C. | 若a为任意实数,则$\sqrt{{a}^{2}}$=a | D. | 若a为任意实数,则($\sqrt{a}$)2=±a |
16.下列各式中,正确的是( )
| A. | $\sqrt{9+4}$=$\sqrt{9}$+$\sqrt{4}$ | B. | $\sqrt{4×9}$=$\sqrt{9}$×$\sqrt{4}$ | C. | $\sqrt{4-2}$=$\sqrt{4}$-$\sqrt{2}$ | D. | $\sqrt{\frac{25}{36}}$=$\sqrt{\frac{5}{6}}$ |