题目内容
16．在离古塔a米的P点，用测角仪测得塔顶的仰角为α，已知测角仪的高度为h米，那么塔高为（ ）| A． | atanα+h | B． | acotα+h | C． | $\sqrt{{a}^{2}+{h}^{2}}$ | D． | （a+h）•cosα |
分析 在Rt△ABE中利用三角函数可以求出BE，然后加上测角仪的高度AP就可以求出铁塔的高度．
解答 解：由题意得，AB=a，∠EAB=α，
在Rt△ABE中，BE=atanα，
而AP=BF=h，
∴铁塔的高度为BF+EB=h+atanα．
故选：A．
点评 本题考查的是解直角三角形的应用-仰角俯角问题，掌握仰角是向上看的视线与水平线的夹角、俯角是向下看的视线与水平线的夹角、熟记锐角三角函数的定义是解题的关键．
练习册系列答案
相关题目
6．
如图，m∥n，△ABC的顶点C在直线m上，若AB=AC，∠A=40°，∠1=20°，则∠2的度数为（ ）
如图，m∥n，△ABC的顶点C在直线m上，若AB=AC，∠A=40°，∠1=20°，则∠2的度数为（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
4．如果$\sqrt{2x-5}$是2x-5的算术平方根，则x的取值范围是（ ）
| A． | x$≥\frac{5}{2}$ | B． | x=$\frac{5}{2}$ | C． | x$≤\frac{5}{2}$ | D． | x$≠\frac{5}{2}$ |
11．直角三角形的两条直角边为a，b，则斜边上的高为（ ）
| A． | $\frac{a+b}{2}$ | B． | $\frac{{a}^{2}+{b}^{2}}{2}$ | ||
| C． | $\frac{\sqrt{{a}^{2}-{b}^{2}}}{2}$ | D． | $\frac{ab\sqrt{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}$ |
1．每个花盆植3株花卉，则每株盈利4元；每个花盆增加1株花卉，平均每株盈利减少0.5元，要使每盆盈利为15元，设每盆多植x株，则x满足方程（ ）
| A． | （3+x）（4-0.5x）=15 | B． | （x+3）（4+0.5x）=15 | C． | （x+4）（3-0.5x）=15 | D． | （x+1）（4-0.5x）=15 |
5．下列叙述正确的是（ ）
| A． | 形如ax2+bx+c=0的方程叫一元二次方程 | |
| B． | 方程4x2+3x=6不含常数项 | |
| C． | （2-x）2=0是一元二次方程 | |
| D． | （a2+1）x2=0不一定是关于x的一元二次方程 |
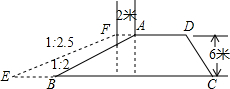如图，有一段水库拦水坝，坝高6m，坝长50m，AD∥BC，沿水库拦水坝的背水坡将坝顶加宽2m，坡度由原来的1：2变成1：2.5．