题目内容
11.已知顶角A等于50°的等腰△ABC内接于⊙O,D是圆周上一点,则∠ADB的度数为65°或115°.分析 根据等腰三角形的性质和三角形内角和定理求出∠ABC和∠ACB的度数,分点D在$\widehat{AC}$或$\widehat{BC}$上和点D在$\widehat{AB}$上三种情况,根据圆周角定理解答即可.
解答  解:∵∠BAC=50°,AB=AC,
解:∵∠BAC=50°,AB=AC,
∴∠ABC=∠ACB=65°,
当点D在$\widehat{AC}$或$\widehat{BC}$上时,∠ADB=∠ACB=65°,
当点D在$\widehat{AB}$上时,∠ADB+∠ACB=180°,解得,∠ADB=115°,
故答案为:65°或115°.
点评 本题考查的是圆周角定理、等腰三角形的性质,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
1.每个花盆植3株花卉,则每株盈利4元;每个花盆增加1株花卉,平均每株盈利减少0.5元,要使每盆盈利为15元,设每盆多植x株,则x满足方程( )
| A. | (3+x)(4-0.5x)=15 | B. | (x+3)(4+0.5x)=15 | C. | (x+4)(3-0.5x)=15 | D. | (x+1)(4-0.5x)=15 |
2.梯形ABCD对角线交于O,AB∥CD,S△BAC:S△AOB=3:1,则,S△AOB:S△COD( )
| A. | 3:1 | B. | 1:2 | C. | 1:4 | D. | 1:9 |
6.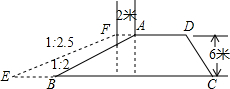 如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
(1)求加宽部分横截面的面积.
(2)完成这一工程需要多少立方米的土?
 如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.(1)求加宽部分横截面的面积.
(2)完成这一工程需要多少立方米的土?
16.下列每组中的两个代数式,不属于同类项的是( )
| A. | $\frac{1}{2}$x2y与$\frac{2}{3}$xy2 | B. | $\frac{1}{2}$m3n与-8nm3 | C. | -3与π | D. | 0.5a2b与πa2b |
3.相异两点A(3,5),B(x,y),若AB∥x轴,则下列结论正确的是( )
| A. | x=3 | B. | y=3 | C. | x=5 | D. | y=5 |
 如图,在建筑物AB上,挂着30m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A,仰角为45°,看条幅底端E处,俯角为30°.求两建筑物间的距离BC(结果精确到0.1m).
如图,在建筑物AB上,挂着30m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A,仰角为45°,看条幅底端E处,俯角为30°.求两建筑物间的距离BC(结果精确到0.1m). 如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为( )
如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为( ) 如图,一次“台风”过后,一根旗杆被台风从高地面5米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断裂前至少有多高?
如图,一次“台风”过后,一根旗杆被台风从高地面5米处吹断,倒下的旗杆的顶端落在离旗杆底部12米处,那么这根旗杆被吹断裂前至少有多高?