题目内容
14.某项工程甲单独做6天完成,乙单独做8天完成,若甲先干一天,然后甲、乙合作完成此项工一共做了x天,则所列方程为( )| A. | $\frac{x+1}{6}$+$\frac{x}{8}$=1 | B. | $\frac{x}{6}$+$\frac{x+1}{8}$=1 | C. | $\frac{x}{6}$+$\frac{x-1}{8}$=1 | D. | $\frac{x}{6}$+$\frac{1}{6}$+$\frac{x-1}{8}$=1 |
分析 合作的天数加1即可确定甲工作的天数,利用总的工作量为1列出方程即可.
解答 解:若甲先干一天,然后甲、乙合作完成此项工一共做了x天,那么甲工作了(x+1)天,
根据题意得:$\frac{x+1}{6}$+$\frac{x}{8}$=1,
故选A.
点评 本题考查了由实际问题抽象出一元一次方程,找到关键描述语,找到等量关系是解决问题的关键.工程问题中常用的关系式有:工作时间=工作总量÷工作效率.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
4.如果$\sqrt{2x-5}$是2x-5的算术平方根,则x的取值范围是( )
| A. | x$≥\frac{5}{2}$ | B. | x=$\frac{5}{2}$ | C. | x$≤\frac{5}{2}$ | D. | x$≠\frac{5}{2}$ |
5.下列叙述正确的是( )
| A. | 形如ax2+bx+c=0的方程叫一元二次方程 | |
| B. | 方程4x2+3x=6不含常数项 | |
| C. | (2-x)2=0是一元二次方程 | |
| D. | (a2+1)x2=0不一定是关于x的一元二次方程 |
2.梯形ABCD对角线交于O,AB∥CD,S△BAC:S△AOB=3:1,则,S△AOB:S△COD( )
| A. | 3:1 | B. | 1:2 | C. | 1:4 | D. | 1:9 |
9. 如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠DEC是( )
如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠DEC是( )
 如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠DEC是( )
如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠DEC是( )| A. | 10° | B. | 12.5° | C. | 15° | D. | 20° |
6.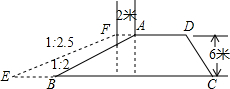 如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
(1)求加宽部分横截面的面积.
(2)完成这一工程需要多少立方米的土?
 如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.
如图,有一段水库拦水坝,坝高6m,坝长50m,AD∥BC,沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1:2变成1:2.5.(1)求加宽部分横截面的面积.
(2)完成这一工程需要多少立方米的土?
3.相异两点A(3,5),B(x,y),若AB∥x轴,则下列结论正确的是( )
| A. | x=3 | B. | y=3 | C. | x=5 | D. | y=5 |
 如图,在建筑物AB上,挂着30m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A,仰角为45°,看条幅底端E处,俯角为30°.求两建筑物间的距离BC(结果精确到0.1m).
如图,在建筑物AB上,挂着30m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A,仰角为45°,看条幅底端E处,俯角为30°.求两建筑物间的距离BC(结果精确到0.1m).