题目内容
1．化简：（x+y）2-3（x2-2y2）=-2x2+2xy+7y2．如果2x÷16y=8，则2x-8y=6．分析 先套用完全平方公式及去括号，再合并同类项即可化简原式；根据幂的运算由2x÷16y=8可得2x-4y=23，即x-4y=3，再整体代入可得．
解答 解：（x+y）2-3（x2-2y2）=x2+2xy+y2-3x2+6y2
=-2x2+2xy+7y2；
∵2x÷16y=8，即2x÷（24）y=8，2x÷24y=8，
∴2x-4y=23，
∴x-4y=3，
则2x-8y=2（x-4y）=6，
故答案为：-2x2+2xy+7y2，6．
点评 本题主要考查整式的混合运算，熟练掌握整式的混合运算法则及根据幂的运算法则由2x÷16y=8得到2x-4y=23是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11．直角三角形的两条直角边为a，b，则斜边上的高为（ ）
| A． | $\frac{a+b}{2}$ | B． | $\frac{{a}^{2}+{b}^{2}}{2}$ | ||
| C． | $\frac{\sqrt{{a}^{2}-{b}^{2}}}{2}$ | D． | $\frac{ab\sqrt{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}$ |
12．某人在高为30米的铁塔AB的塔顶A处，向正东方向观察地面上的C处和D处，俯角分别是30°和60°．如果B、D、C成一直线，那么C处和D处之间的距离，可以是下列数据中的（ ）
| A． | 20$\sqrt{3}$米 | B． | 30$\sqrt{3}$米 | C． | 40$\sqrt{3}$米 | D． | 50$\sqrt{3}$米 |
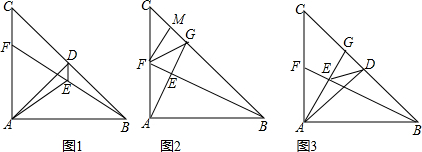
9．
如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠DEC是（ ）
如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠DEC是（ ）| A． | 10° | B． | 12.5° | C． | 15° | D． | 20° |
16．若点A（1，y1），B（2，y2），C（3，y3）在反比例函数y=$\frac{{k}^{2}+1}{x}$的图象上，则（ ）
| A． | y1＜y2＜y3 | B． | y1＞y2＞y3 | C． | y1＜y3＜y2 | D． | y1=y2=y3 |
6．
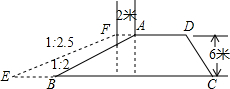如图，有一段水库拦水坝，坝高6m，坝长50m，AD∥BC，沿水库拦水坝的背水坡将坝顶加宽2m，坡度由原来的1：2变成1：2.5．
（1）求加宽部分横截面的面积．
（2）完成这一工程需要多少立方米的土？
如图，有一段水库拦水坝，坝高6m，坝长50m，AD∥BC，沿水库拦水坝的背水坡将坝顶加宽2m，坡度由原来的1：2变成1：2.5．（1）求加宽部分横截面的面积．
（2）完成这一工程需要多少立方米的土？
13．
a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，-a，b，-b，a+b，a-b按照从小到大的顺序排列，正确的是（ ）
a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，-a，b，-b，a+b，a-b按照从小到大的顺序排列，正确的是（ ）| A． | a-b＜a＜-b＜b-a＜-a＜b | B． | -b＜a-b＜-a＜a＜b-a＜b | ||
| C． | a＜-b＜a-b＜-a＜b＜b-a | D． | a-b＜-b＜a＜-a＜b＜b-a |
10．已知△ABC的周长为1，连接△ABC三边的中点构成第二个三角形，再连接第二个三角形三边的中点构成第三个三角形，依此类推，则第2014个三角形的周长为（ ）
| A． | $\frac{1}{{2}^{2014}}$ | B． | $\frac{1}{{2}^{2013}}$ | C． | $\frac{1}{2014}$ | D． | $\frac{1}{2013}$ |
