题目内容
8.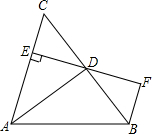 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.(1)探索AB与BF的数量关系,说明理由.
(2)若BF=1,求BC的长.
分析 (1)首先证明AC=AB,再证明△CDE≌△DBF,推出DE=DF,CE=BF,由题意AE=2BF,AC=AB=3BF.
(2)只要证明△CED∽△CDA,得CD2=CE•CA,由此即可解决问题.
解答 解:(1)结论:AB=3BF.
理由:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD平分∠BAC,
∴DC=BD,
在△CDE与△DBF中,
$\left\{\begin{array}{l}{∠C=∠CBF}\\{CD=BD}\\{∠EDC=∠BDF}\end{array}\right.$,
∴△CDE≌△DBF(ASA),
∴DE=DF,CE=BF,
∵AE=2BF,
∴AC=3BF,
∴AB=3BF.
(2)∵AC=AB,CD=BD,DE⊥AC,
∴AD⊥BC,
∴∠CDA=∠CED=90°,∵∠C=∠C,
∴△CED∽△CDA,
∴CD2=CE•CA,
∵CE=BF=1,AC=3BF=3,
∴CD2=3,
∴CD=$\sqrt{3}$,
∴BC=2CD=2$\sqrt{3}$.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,勾股定理等知识,掌握等腰三角形的性质三线合一是解题的关键.

练习册系列答案
相关题目
16.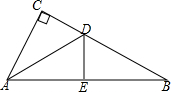 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
20. 如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
 如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
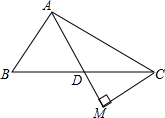 在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)
在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA) 如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.
如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.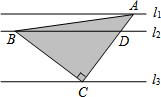 如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为$\frac{25}{2}$.
如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为$\frac{25}{2}$.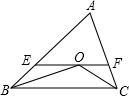 △ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.