题目内容
7.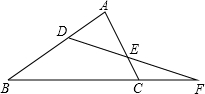 如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°.
如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=87°.
分析 由已知根据三角形内角和定理可求出△ABC中∠A的度数,同理可求出△ADE中∠ADE的度数,再由∠ADE+∠BDF=180°求出∠BDF.
解答 解:在△ABC中,∠A=180°-∠B-∠ACB=180°-67°-74°=39°,
在△ADE中,∠ADE=180°-∠A-∠AED=180°-39°-48°=93°,
∴∠BDF=180°-∠ADE=180°-93°=87°.
故答案为:87°.
点评 此题考查的是三角形内角和定理,解决问题的关键是掌握三角形内角和定理:三角形内角和是180°.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
5.一组数据1,3,5,8,x的中位数是5,则下列x的取值中,满足条件的是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
12.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
| A. | $\sqrt{2}$:1 | B. | 4:1 | C. | 3:1 | D. | 2:1 |
16.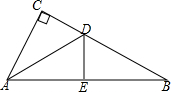 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
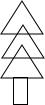 如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.
如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.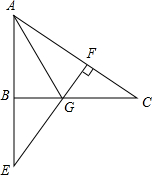 如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.
如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.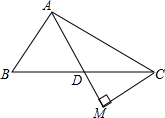 在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)
在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)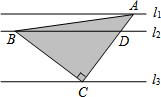 如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为$\frac{25}{2}$.
如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为$\frac{25}{2}$.