题目内容
1. 如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.
如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.
分析 根据轴对称的性质可得PA=P1A,PB=P2B,然后求出△PAB的周长=P1P2.
解答 解:∵P点关于m、n的对称点P1、P2,
∴PA=P1A,PB=P2B,
∴△PAB的周长=PA+AB+PB=P1A+AB+P2B=P1P2,
∵△PAB的周长是10,
∴P1P2=10.
故答案为:10.
点评 本题考查了轴对称的性质,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等.

练习册系列答案
相关题目
12.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
| A. | $\sqrt{2}$:1 | B. | 4:1 | C. | 3:1 | D. | 2:1 |
9.下列三角形中,能全等的是( )
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
| A. | (1)(3) | B. | (2)(4) | C. | (1)(4) | D. | (1)(3)(4) |
16.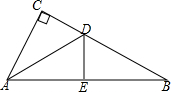 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
 如图,∠A=∠B,CE∥DA,CE交AB于E.
如图,∠A=∠B,CE∥DA,CE交AB于E.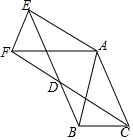 △ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点, 作出图中的三角形关于y轴的轴对称图形,并写出点A关于y轴对称的点的坐标.
作出图中的三角形关于y轴的轴对称图形,并写出点A关于y轴对称的点的坐标.