题目内容
5. 长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.
长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.
分析 由操作的程序找出第一、二次操作后剩下纸片的相邻两边长度,根据第三次操作后剩下纸片为正方形找出第二次操作后两边长之间存在2倍关系,由此即可得出关于a的一元一次方程,解之即可得出结论.
解答 解:第一次操作后,剩下的长方形纸片长为a,宽为(2-a),
第二次操作后,剩下的长方形的相邻两边长为(2-a)和(2a-2),
∵第三次操作后,剩下的纸片为正方形,
∴2-a=2(2a-2)或2a-2=2(2-a),
解得:a=$\frac{6}{5}$或a=$\frac{3}{2}$.
故答案为:$\frac{6}{5}$或$\frac{3}{2}$.
点评 本题考查了一元一次方程的应用以及列代数式,根据操作的程序找出“若第n次操作后剩下纸片为正方形,则第(n-1)次操作后剩余纸片相邻两边存在2倍关系”是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
16.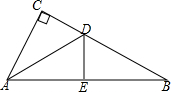 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
20. 如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
 如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
15.当x=2时,代数式ax3+bx+1的值为6,那么当x=-2时,这个代数式的值是( )
| A. | 1 | B. | -4 | C. | 4 | D. | -6 |
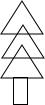 如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.
如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.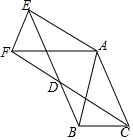 △ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,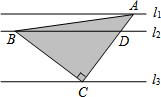 如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为$\frac{25}{2}$.
如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为$\frac{25}{2}$.