题目内容
11.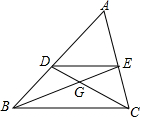 如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
如图,在△ABC中,中线BE、CD相交于点G,则$\frac{DE}{BC}$=$\frac{1}{2}$;S△DEG:S△ABC=1:12.
分析 由BE、CD是△ABC的中线,可得DE是△ABC的中位线,然后由三角形中位线的性质,可得△GDE∽△GCB,△ADE∽△ABC,得出S△GCB=4S△GDE,S△ABC=4S△ADE,即可得出结论.
解答 解:∵BE、CD是△ABC的中线,
∴DE∥BC,DE=$\frac{1}{2}$BC,AE=EC,
∴$\frac{DE}{BC}$=$\frac{1}{2}$,△GDE∽△GCB,△ADE∽△ABC,
∴$\frac{GE}{GB}=\frac{DE}{BC}$=$\frac{1}{2}$,S△GCB=4S△GDE,S△ABC=4S△ADE,
∴S△BDG=S△CEG=2S△GDE,
∴S△DEG:S△ABC=1:12;
故答案为:$\frac{1}{2}$,1:12.
点评 此题考查了相似三角形的判定与性质、三角形中位线的性质以及三角形的面积.此题难度适中,注意掌握等高三角形的面积比等于对应底的比性质的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
16.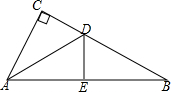 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
 如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )
如图,已知,在△ABC中,∠C=90°,AC=AE,DE⊥AB于点E,且∠CDA=50°,则∠BDE的度数为( )| A. | 40° | B. | 50° | C. | 10° | D. | 80° |
20. 如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
 如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )
如图所示,用一副三角尺拼成的图形中,若∠BAE=135°,则∠CAD的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
1.下列各数中是无理数的是( )
| A. | 1.$\stackrel{•}{3}$$\stackrel{•}{4}$ | B. | $\frac{22}{7}$ | C. | $\sqrt{16}$ | D. | 0.020020002… |
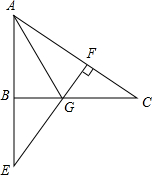 如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.
如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.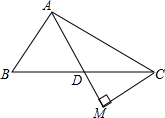 在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)
在△ABC中AD平分∠BAC,AD=AB,CM⊥AD,垂足为M,求证:AM=$\frac{1}{2}$(AB+CA)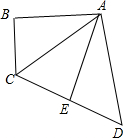 如图,在四边形ABCD中,∠B=90°,点E是CD的中点,连结AE,AC,且AC=AD,AB=AE.
如图,在四边形ABCD中,∠B=90°,点E是CD的中点,连结AE,AC,且AC=AD,AB=AE. 如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.
如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.