题目内容
6.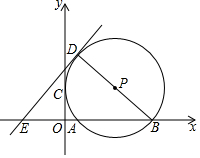 如图,已知⊙P与x轴交于A和B(9,0)两点,与y轴的正半轴相切与点C(0,3),作⊙P的直径BD,过点D作直线DE⊥BD,交x轴于E点,若点P在双曲线y=$\frac{15}{x}$上,则直线DE的解析式为y=$\frac{12}{7}$x+$\frac{30}{7}$.
如图,已知⊙P与x轴交于A和B(9,0)两点,与y轴的正半轴相切与点C(0,3),作⊙P的直径BD,过点D作直线DE⊥BD,交x轴于E点,若点P在双曲线y=$\frac{15}{x}$上,则直线DE的解析式为y=$\frac{12}{7}$x+$\frac{30}{7}$.
分析 连接PC.AD,过P作PE⊥AB于E,根据已知条件得到OB=9,OC=3,根据切线的性质得到PC⊥y轴,推出四边形OEPC是矩形,得到PE=OC=3,求得P(5,3),得到PC=5,BD=10,根据三角形的中位线的性质得到D(1,6),根据相似三角形的性质得到E(-$\frac{7}{2}$,0),设直线DE的解析式为y=kx+b,代入数据即可得到结论.
解答 解:连接PC.AD,过P作PE⊥AB于E,
∵C(0,3),B(9,0),
∴OB=9,OC=3,
∵⊙P与y轴的正半轴相切与点C,
∴PC⊥y轴,
∴四边形OEPC是矩形,
∴PE=OC=3,
把y=3代入y=$\frac{15}{x}$得,x=5,
∴P(5,3),
∴PC=5,BD=10,
∵BD是⊙P的直径,
∴AD⊥x轴,
∴PE∥AD,
∵P是BD的中点,
∴AD=6,
∴AB=8,
∴OA=1,
∴D(1,6),
∵DE⊥BD,
∴∠EDA+∠BDA=∠AED+∠EDA=90°,
∴∠AED=∠ADB,
∴△ADE∽△ABD,
∴$\frac{AE}{AD}=\frac{AD}{AB}$,
∴AE=$\frac{9}{2}$,
∴E(-$\frac{7}{2}$,0),
设直线DE的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{0=-\frac{7}{2}k+b}\\{6=k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=\frac{14}{3}}\end{array}\right.$,
∴直线DE的解析式为y=$\frac{4}{3}$x+$\frac{14}{3}$.
故答案为:y=$\frac{4}{3}$x+$\frac{14}{3}$.
点评 本题考查了反比例函数与一次函数的交点的问题,切线的性质,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案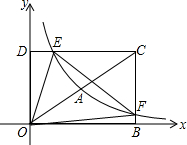 如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.
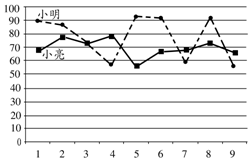 小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )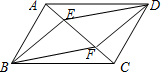 如图,已知?ABCD,BE⊥AC于点E,DF⊥AC于点F,连接DE、BF,求证:DE=BF.
如图,已知?ABCD,BE⊥AC于点E,DF⊥AC于点F,连接DE、BF,求证:DE=BF.