题目内容
7.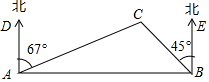 一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).
一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42,$\sqrt{2}$=1.41】
分析 作CD⊥AB,在Rt△ADC中由sin23°=$\frac{CD}{AC}$求得CD=3.9,在Rt△BCD中由sin45°=$\frac{CD}{BC}$求得BC=$\sqrt{2}$CD,即可得出答案.
解答 解:过点C作CD⊥AB于点D,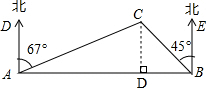
由题意,得:∠BAC=23°,∠ABC=45°,AC=10,
在Rt△ADC中,∠ADC=90°,
∴sin23°=$\frac{CD}{AC}$=0.39,
∴CD=10×0.39=3.9,
在Rt△BCD中,∠CDB=90°,
∴sin45°=$\frac{CD}{BC}$=$\frac{\sqrt{2}}{2}$,
∴BC=$\sqrt{2}$CD=1.41×3.9=5.499≈5.5,
答:码头B与小岛C的距离是5.5海里.
点评 本题考查了解直角三角形的应用-方向角问题,作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
12. 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )
 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=50°,则∠CAD的大小为( )| A. | 50° | B. | 65° | C. | 80° | D. | 60° |
 如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为$\frac{\sqrt{5}}{5}$.
如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为$\frac{\sqrt{5}}{5}$.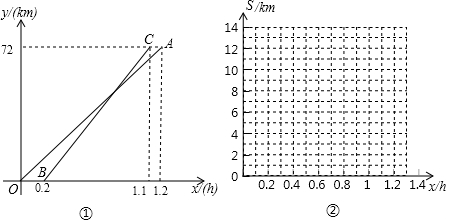
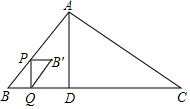 如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).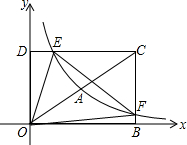 如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.