题目内容
12.计算:(1)-32+(π-3.1)0-|1-3$\frac{1}{2}$|×(-$\frac{1}{2}$)-1
(2)(-2x)2•(x2)3÷(-x)2
(3)(x-4)x-(x-1)(x+2)
(4)利用乘法公式计算1232-124×122.
分析 (1)原式利用乘方的意义,零指数幂、负整数指数幂法则,以及绝对值的代数意义化简即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;
(3)原式利用单项式乘以多项式,多项式乘以多项式法则计算,去括号合并即可得到结果;
(4)原式变形后,利用平方差公式计算即可得到结果.
解答 解:(1)原式=-9+1+5=-3;
(2)原式=4x2•x6÷x2=4x6;
(3)原式=x2-4x-x2-2x+x+2=-5x+2;
(4)原式=1232-(123+1)×(123-1)=1232-1232+1=1.
点评 此题考查了整式的混合运算,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 已知关于x的不等式x-a≥-2的解集在数轴上表示如图,则a的值为1.
已知关于x的不等式x-a≥-2的解集在数轴上表示如图,则a的值为1.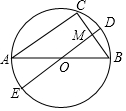 如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于点M.若点E在优弧$\widehat{CAB}$上,AC=8,BC=6,则EM=9.
如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于点M.若点E在优弧$\widehat{CAB}$上,AC=8,BC=6,则EM=9.