题目内容
7.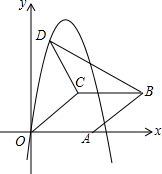 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
分析 设D(x,-x2+6x),根据勾股定理求得OC,根据菱形的性质得出BC,然后根据三角形面积公式得出∴S△BCD=$\frac{1}{2}$×5×(-x2+6x-3)=-$\frac{5}{2}$(x-3)2+15,根据二次函数的性质即可求得最大值.
解答 解:∵D是抛物线y=-x2+6x上一点,
∴设D(x,-x2+6x),
∵顶点C的坐标为(4,3),
∴OC=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵四边形OABC是菱形,
∴BC=OC=5,BC∥x轴,
∴S△BCD=$\frac{1}{2}$×5×(-x2+6x-3)=-$\frac{5}{2}$(x-3)2+15,
∵-$\frac{5}{2}$<0,
∴S△BCD有最大值,最大值为15,
点评 本题考查了菱形的性质,二次函数的性质,注意数与形的结合是解决本题的关键.

练习册系列答案
相关题目
18.若一等腰三角形的底边为2,底边上的高是$\sqrt{3}$,则其顶角的大小为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
19.(-3)2的平方根是( )
| A. | -3 | B. | 3 | C. | 3或-3 | D. | 9 |
16. 如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )
如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )
 如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )
如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )| A. | 66° | B. | 104° | C. | 114° | D. | 124° |
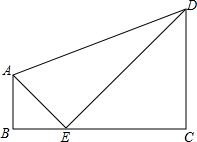 如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,
如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,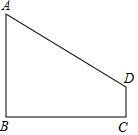 如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.
如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.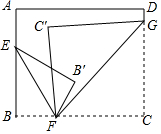 如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.
如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°. 列方程或方程组解应用题:
列方程或方程组解应用题: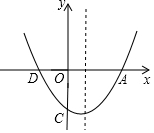 如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).
如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).