题目内容
12．
列方程或方程组解应用题：公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图阴影部分），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为20m2，求原正方形空地的边长．
分析 可设原正方形的边长为xm，则剩余的空地长为（x-1）m，宽为（x-2）m．根据长方形的面积公式方程可列出，进而可求出原正方形的边长．
解答 解：设原正方形空地的边长为xm，
根据题意，得 （x-1）（x-2）=20，
解方程，得 x1=6，x2=-3（舍），
答：原正方形空地的边长为6m．
点评 本题考查了一元二次方程的应用，应熟记长方形的面积公式．另外求得剩余的空地的长和宽是解决本题的关键．
练习册系列答案
相关题目
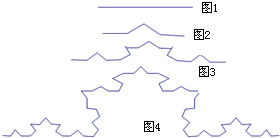若图1中的线段长为1，将此线段三等分，并以中间的一段为边作等边三角形，然后去掉这一段，得到图2称第1次操作，再将图2中的每一段类似变形，得到图3即第2次操作，按上述方法继续得到图4为第3次操作，则第4次操作后折线的总长度为$\frac{64}{27}$．
3．一元二次方程x2+x-1=0 的根的情况为（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 只有一个实数根 | D． | 没有实数根 |
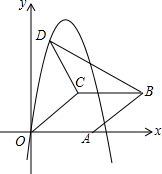如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D是抛物线y=-x2+6x上一点，且在x轴上方，则△BCD面积的最大值是多少？
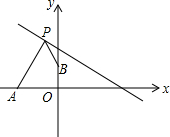如图，点A的坐标为（-2，0），点B的坐标为（0，1），点P在直线y=-$\frac{1}{2}$x+2上运动，当线段|AP-BP|最长时，点P的坐标是（1，$\frac{3}{2}$）．
4．已知y与x-1成反比例，那么它的解析式为（ ）
| A． | y=$\frac{k}{x}$-1（k≠0） | B． | y=k（x-1）（k≠0） | C． | y=$\frac{k}{x-1}$（k≠0） | D． | y=$\frac{x-1}{k}$（k≠0） |
1．二次根式$\sqrt{x-\sqrt{2}}$中x的取值范围是（ ）
| A． | x≥$\sqrt{2}$ | B． | x≤$\sqrt{2}$ | C． | x＜$\sqrt{2}$ | D． | x＞$\sqrt{2}$ |
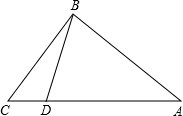如图，在Rt△ABC中，∠ABC=90°，AB=20，BC=15，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，设点D运动的时间为t秒，速度为每秒2个单位长度．