题目内容
18.若一等腰三角形的底边为2,底边上的高是$\sqrt{3}$,则其顶角的大小为( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
分析 依照题意画出图形,由等腰三角形的性质可得出BD=$\frac{1}{2}$BC=1,利用勾股定理即可得出AB的长度,再根据“在直角三角形中,30°角所对的直角边等于斜边的一半”即可得出∠BAD=30°,进而得出结论.
解答 解:依照题意画出图形,如图所示.
∵BC=2,AD=$\sqrt{3}$,△ABC为等腰三角形,
∴BD=$\frac{1}{2}$BC=1,AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=2,
∴BD=$\frac{1}{2}$AB.
∴∠BAD=30°,
∴∠BAC=2∠BAD=60°.
故选A.
点评 本题考查了等腰三角形的性质、勾股定理以及含30度角的直角三角形,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”找出∠BAD的度数是解题的关键(注:若是高年级可以用正、余切求角).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某校初一数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如表所示:
根据表格提供的信息,下列说法错误的是( )
| 支撑物高度h/cm | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 小车下滑时间t/s | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 |
| A. | 支撑物的高度为40cm,小车下滑时间为2.13s | |
| B. | 支撑物高度h越大,小车下滑时间t越小 | |
| C. | 若小车下滑时间为2s,则支撑物高度在40cm至50cm之间 | |
| D. | 若支撑物的高度为80cm,则小车下滑时间可以使小于1.59s的任意值 |
9.下列三角形中,能全等的是( )
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
| A. | (1)(3) | B. | (2)(4) | C. | (1)(4) | D. | (1)(3)(4) |
3.一元二次方程x2+x-1=0 的根的情况为( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
 如图,∠A=∠B,CE∥DA,CE交AB于E.
如图,∠A=∠B,CE∥DA,CE交AB于E.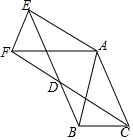 △ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,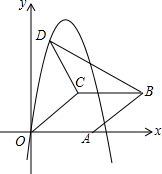 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?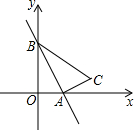 已知:如图,一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B,以线段AB为直角边作Rt△ABC,且∠ABC=30°,∠BAC=90°,点C在第一象限
已知:如图,一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B,以线段AB为直角边作Rt△ABC,且∠ABC=30°,∠BAC=90°,点C在第一象限