题目内容
17.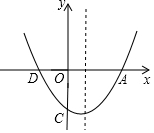 如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).
如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).(1)求该抛物线的函数解析式;
(2)求出A,D两点的坐标.
(3)若点M在抛物线上,且△MAD的面积等于△COD的面积的3倍,求点M的坐标.
分析 (1)设抛物线的解析式为y=a(x-1)2-$\frac{27}{8}$,把(0,-3)的坐标代入,求出a即可.
(2)令y=0,得$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=0,解方程即可.
(3)设M(m,n),由题意$\frac{1}{2}$×6×|n|=3×$\frac{1}{2}$×2×3,解得n=±3,对于抛物线y=$\frac{3}{8}$(x-1)2-$\frac{27}{8}$,当y=3时,$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=3,求出x的值.当y=-3时,$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=-3,求出x的值即可.
解答 解:(1)设抛物线的解析式为y=a(x-1)2-$\frac{27}{8}$,
把(0,-3)的坐标代入,得a=$\frac{3}{8}$,
∴抛物线的解析式为y=$\frac{3}{8}$(x-1)2-$\frac{27}{8}$.
(2)令y=0,得$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=0,解得x=-2或4,
∴A(4,0),D(-2,0).
(3)设M(m,n),
由题意$\frac{1}{2}$×6×|n|=3×$\frac{1}{2}$×2×3,
解得n=±3,
对于抛物线y=$\frac{3}{8}$(x-1)2-$\frac{27}{8}$,
当y=3时,$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=3,解得x=1$±\sqrt{17}$,
∴M(1+$\sqrt{17}$,3)或(1-$\sqrt{17}$,3),
当y=-3时,$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=-3,解得x=2或0,
∴M(0,-3)或(2,-3),
综上所述,满足条件的点M的坐标为M(1+$\sqrt{17}$,3)或(1-$\sqrt{17}$,3)或(0,-3)或(2,-3).
点评 本题考查抛物线与x轴的交点、待定系数法求二次函数解析式等知识,解题的关键是掌握二次函数的三种形式,学会构建方程解决问题,属于中考常考题型.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案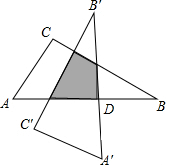 如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
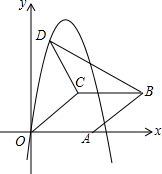 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?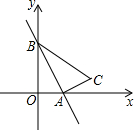 已知:如图,一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B,以线段AB为直角边作Rt△ABC,且∠ABC=30°,∠BAC=90°,点C在第一象限
已知:如图,一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B,以线段AB为直角边作Rt△ABC,且∠ABC=30°,∠BAC=90°,点C在第一象限 某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:
某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题: 如图,BC=50,∠ABC=45°,∠ACB=30°,求点A到BC的距离.
如图,BC=50,∠ABC=45°,∠ACB=30°,求点A到BC的距离.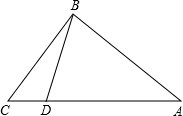 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.