题目内容
16. 如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )
如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )| A. | 66° | B. | 104° | C. | 114° | D. | 124° |
分析 由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC,由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=$\frac{1}{2}$∠1=22°,再由三角形内角和定理求出∠B即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=$\frac{1}{2}$∠1=22°,
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°.
故选:C.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.

练习册系列答案
相关题目
4.已知y与x-1成反比例,那么它的解析式为( )
| A. | y=$\frac{k}{x}$-1(k≠0) | B. | y=k(x-1)(k≠0) | C. | y=$\frac{k}{x-1}$(k≠0) | D. | y=$\frac{x-1}{k}$(k≠0) |
1.二次根式$\sqrt{x-\sqrt{2}}$中x的取值范围是( )
| A. | x≥$\sqrt{2}$ | B. | x≤$\sqrt{2}$ | C. | x<$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
6.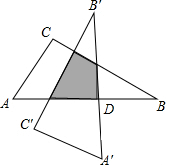 如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
 如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
 如图,∠A=∠B,CE∥DA,CE交AB于E.
如图,∠A=∠B,CE∥DA,CE交AB于E.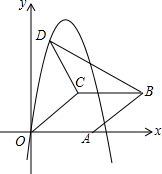 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少? 作出图中的三角形关于y轴的轴对称图形,并写出点A关于y轴对称的点的坐标.
作出图中的三角形关于y轴的轴对称图形,并写出点A关于y轴对称的点的坐标.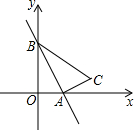 已知:如图,一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B,以线段AB为直角边作Rt△ABC,且∠ABC=30°,∠BAC=90°,点C在第一象限
已知:如图,一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B,以线段AB为直角边作Rt△ABC,且∠ABC=30°,∠BAC=90°,点C在第一象限 某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:
某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题: