题目内容
19.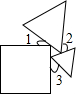 一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )| A. | 180° | B. | 100° | C. | 90° | D. | 80° |
分析 设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.
解答  解:如图,∠BAC=180°-90°-∠1=90°-∠1,
解:如图,∠BAC=180°-90°-∠1=90°-∠1,
∠ABC=180°-60°-∠3=120°-∠3,
∠ACB=180°-60°-∠2=120°-∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°-∠1+120°-∠3+120°-∠2=180°,
∴∠1+∠2=150°-∠3,
∵∠3=60°,
∴∠1+∠2=150°-60°=90°.
故选C.
点评 本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
9. 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
7.如图,∠1和∠2是对顶角的图形是( )


| A. | 甲 | B. | 丙 | C. | 丁 | D. | 乙 |
11.如图1,在五边形ABCDE中,AE∥BC,∠A=∠C.
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)延长DE至F,连接BE,如图2,若∠1=∠3,∠AEF=2∠2,求证:∠AED=∠C.
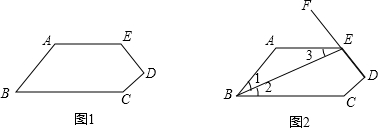
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)延长DE至F,连接BE,如图2,若∠1=∠3,∠AEF=2∠2,求证:∠AED=∠C.

8. 将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )
将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )
 将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )
将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )| A. | 120° | B. | 130° | C. | 135° | D. | 150° |
9.方程5x-$\frac{1}{6}$=4x-$\frac{1}{3}$的解是( )
| A. | x=$\frac{1}{6}$ | B. | x=-$\frac{1}{6}$ | C. | x=$\frac{1}{2}$ | D. | 以上答案都不是 |
 将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.
将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.
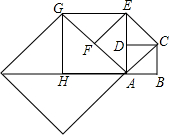 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.