题目内容
4.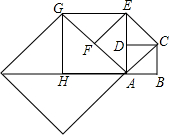 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.
分析 首先求出AC、AE、HE的长度,然后猜测命题中隐含的数学规律,即可解决问题.
解答 解:∵四边形ABCD为正方形,
∴AB=BC=1,∠B=90°,
∴AC2=12+12,AC=$\sqrt{2}$;
同理可求:AE=($\sqrt{2}$)2,HE=($\sqrt{2}$)3…,
∴第n个正方形的边长an=($\sqrt{2}$)n-1.
故答案为($\sqrt{2}$)n-1.
点评 该题主要考查了正方形的性质、勾股定理及其应用问题;应牢固掌握正方形有关定理并能灵活运用.

练习册系列答案
相关题目
14.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{9}$ |
15.点P为直线l外一点,点A、B、C为直线上三点,PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为( )
| A. | 2cm | B. | 3cm | C. | 小于3cm | D. | 不大于3cm |
19.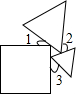 一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
 一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=60°,则∠1+∠2=( )| A. | 180° | B. | 100° | C. | 90° | D. | 80° |
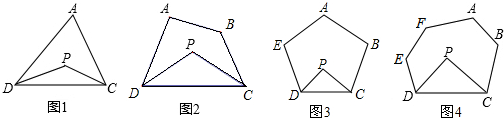
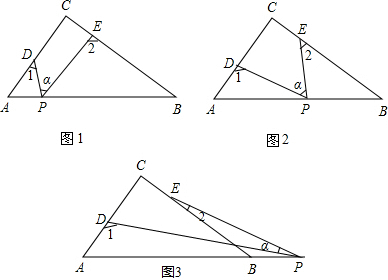
 一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,
一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,