题目内容
9.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 求出扇形的弧长,根据圆锥的底面圆周长是扇形的弧长计算即可.
解答 解:扇形的弧长=$\frac{120π×12}{180}$=8π,即圆锥的底面周长为8π,
∴它的底面圆的半径=$\frac{8π}{2π}$=4,
故选:B.
点评 本题考查的是圆锥的计算,掌握圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长是解题的关键.

练习册系列答案
相关题目
17.某商场经营一批进价是30元/件的商品,在市场试销中的日销售量y件与销售价x元之间满足一次函数关系.?
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;?
(2)若日销售利润为P元,根据上述关系写出P关于x的函数关系式,并指出当销售单价x为多少元时,才能获得最大的销售利润?
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;?
| x | 35 | 40 | 45 | 50 |
| y | 57 | 42 | 27 | 12 |
18.某超市在50天内试销一款成本40元/件的新型商品,了解到此款商品第x天的销售信息如下表:
(1)当第5或45天时,该商品的销售单价为65元/件;
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
| 销售量P(件) | p=120-2x |
| 销售单价q(元/件) | 当1≤x<25时,q=x+60; 当25≤x≤50时,q=40+$\frac{1125}{x}$ |
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
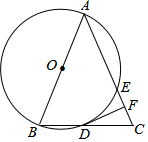 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.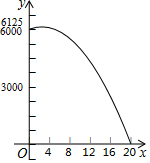 某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题:
某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题: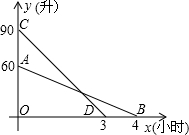 “滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.
“滴滴出行”是一款涵盖出租车、专车、快车、顺风车等多项业务在内的一站式出行平台,如今已成为人们出行常用的“打车神器”,如图,分别是“滴滴出行”旗下甲、乙两辆轿车某天油箱中的剩余油量y(升)与行驶时间x(小时)的函数图象.