题目内容
4.圆锥底面圆的半径为3,高长为4,它的表面积等于24π(结果保留π).分析 根据圆的面积公式、扇形的面积公式计算即可.
解答 解:圆锥的母线长=$\sqrt{{3}^{2}+{4}^{2}}$=5,
圆锥底面圆的面积=9π
圆锥底面圆的周长=2×π×3=6π,即扇形的弧长为6π,
∴圆锥的侧面展开图的面积=$\frac{1}{2}×$6π×5=15π,
15π+9π=24π
故答案为:24π.
点评 本题考查的是圆锥的计算,掌握圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,注意圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
1.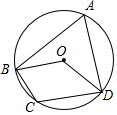 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )| A. | π | B. | $\frac{3}{2}π$ | C. | 2π | D. | 3π |
9.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
13.某商场经市场调查,发现进价为40元的某童装每月的销售量y(件)与售价x(元)的相关信息如下:
(1)试用你学过的函数来描述y与x的关系,这个函数可以是一次函数(填一次函数、反比例函数或二次函数),求这个函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?
| 售价x(元) | 60 | 70 | 80 | 90 | … |
| 销售量y(件) | 280 | 260 | 240 | 220 | … |
(2)售价为多少元时,当月的利润最大?最大利润是多少?
 如图,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA=36度.
如图,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA=36度. 如图,菱形ABCD的周长为24cm,正方形AECF的周长为16cm,则菱形的面积为8$\sqrt{14}$cm2.
如图,菱形ABCD的周长为24cm,正方形AECF的周长为16cm,则菱形的面积为8$\sqrt{14}$cm2.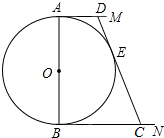 如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.