题目内容
6.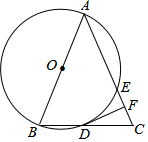 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.(1)求证:DF是⊙O的切线;
(2)若AE=4,cosA=$\frac{2}{5}$,求DF的长.
分析 (1)证明:如图,连接OD,作OG⊥AC于点G,推出∠ODB=∠C;然后根据DF⊥AC,∠DFC=90°,推出∠ODF=∠DFC=90°,即可推出DF是⊙O的切线.
(2)首先判断出:AG=$\frac{1}{2}$AE=2,然后判断出四边形OGFD为矩形,即可求出DF的值是多少.
解答 (1)证明:如图,连接OD,作OG⊥AC于点G,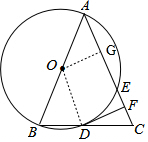 ,
,
∵OB=OD,
∴∠ODB=∠B,
又∵AB=AC,
∴∠C=∠B,
∴∠ODB=∠C,
∵DF⊥AC,
∴∠DFC=90°,
∴∠ODF=∠DFC=90°,
∴DF是⊙O的切线.
(2)解:AG=$\frac{1}{2}$AE=2,
∵cosA=$\frac{AG}{OA}$,
∴OA=$\frac{AG}{cosA}$=$\frac{2}{\frac{2}{5}}$=5,
∴OG=$\sqrt{{OA}^{2}{-AG}^{2}}$=$\sqrt{21}$,
∵∠ODF=∠DFG=∠OGF=90°,
∴四边形OGFD为矩形,
∴DF=OG=$\sqrt{21}$.
点评 此题主要考查了切线的性质和应用,等腰三角形的性质和应用,以及解直角三角形的应用,要熟练掌握.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
17.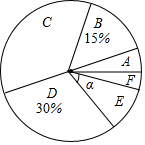 今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.
今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.
请根据图表提供的信息,解答下列问题:
(1)本次抽样调查样本容量为80,表中:m=12,n=8;扇形统计图中,E等级对应扇形的圆心角α等于36度;
(2)该校决定从本次抽取的A等级学生(记为甲、乙、病、丁)中,随机选择2名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
 今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.
今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.| 等级 | 得分x(分) | 频数(人) |
| A | 95≤x≤100 | 4 |
| B | 90≤x<95 | m |
| C | 85≤x<90 | n |
| D | 80≤x<85 | 24 |
| E | 75≤x<80 | 8 |
| F | 70≤x<75 | 4 |
(1)本次抽样调查样本容量为80,表中:m=12,n=8;扇形统计图中,E等级对应扇形的圆心角α等于36度;
(2)该校决定从本次抽取的A等级学生(记为甲、乙、病、丁)中,随机选择2名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
1.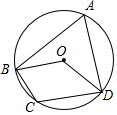 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )| A. | π | B. | $\frac{3}{2}π$ | C. | 2π | D. | 3π |
8.现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
(1)根据题意,填写下表:
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
(3)小明应选择哪家快递公司更省钱?
9.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
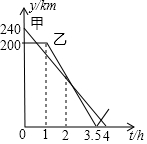 在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地.在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2$\frac{5}{7}$h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是②③④(填写所有正确结论的序号).
在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地.在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2$\frac{5}{7}$h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是②③④(填写所有正确结论的序号).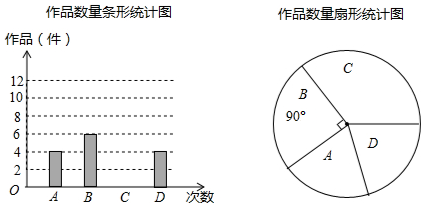
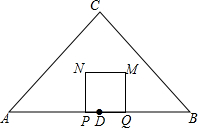 如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4,点D是AB的中点,动点P、Q同时从点D出发(点P、Q不与点D重合),点P沿D→A以1cm/s的速度向中点A运动.点Q沿D→B→D以2cm/s的速度运动.回到点D停止.以PQ为边在AB上方作正方形PQMN,设正方形PQMN与△ABC重叠部分的面积为S(cm2),点P运动的时间为t(s).
如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4,点D是AB的中点,动点P、Q同时从点D出发(点P、Q不与点D重合),点P沿D→A以1cm/s的速度向中点A运动.点Q沿D→B→D以2cm/s的速度运动.回到点D停止.以PQ为边在AB上方作正方形PQMN,设正方形PQMN与△ABC重叠部分的面积为S(cm2),点P运动的时间为t(s).