题目内容
17.某商场经营一批进价是30元/件的商品,在市场试销中的日销售量y件与销售价x元之间满足一次函数关系.?(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;?
| x | 35 | 40 | 45 | 50 |
| y | 57 | 42 | 27 | 12 |
分析 (1)根据待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”得到函数解析式,配方成顶点式即可得其最大值.
解答 解:(1)因日销售量y件与销售价x元满足一次函数,
故一次函数设为:y=ax+b,
由题意得:
$\left\{\begin{array}{l}{45a+b=27}\\{50a+b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=162}\end{array}\right.$,
故y=162-3x为所求的函数关系式,
∵y≥0,
∴0≤x≤54.
?(2)依题意得:P=(x-30)•y=(x-30)•(162-3x)=-3(x-42)2+432.
当x=42时,ymax=432,
即销售单价为42元/件时,获最大日销售利润432元.
答:当销售单价x为42元时,才能获得最大的销售利润.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法和依据相等关系列出函数解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
(1)根据题意,填写下表:
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
(3)小明应选择哪家快递公司更省钱?
9.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
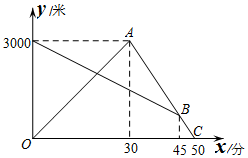 某天早晨,小刚从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,小刚跑到体育场后发现要下雨,立即以另一速度按原路返回,遇到妈妈后,妈妈立即以小刚返回的速度和小刚一起回家(妈妈与小刚行进的路线相同).如图是两人离家的距离y(米)与小刚出发的时间x(分)之间的函数图象,则小刚第一次和妈妈相遇时,妈妈离家的距离为2000 米.
某天早晨,小刚从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,小刚跑到体育场后发现要下雨,立即以另一速度按原路返回,遇到妈妈后,妈妈立即以小刚返回的速度和小刚一起回家(妈妈与小刚行进的路线相同).如图是两人离家的距离y(米)与小刚出发的时间x(分)之间的函数图象,则小刚第一次和妈妈相遇时,妈妈离家的距离为2000 米. 如图,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA=36度.
如图,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA=36度. △ABC中,D、E分别在AB、AC上,DE∥BC,AD=1,BD=3,则△ADE与△ABC的面积之比为1:16.
△ABC中,D、E分别在AB、AC上,DE∥BC,AD=1,BD=3,则△ADE与△ABC的面积之比为1:16. 如图,矩形ABCD的对角线AC,BD相交于点O,分别过点C,D作BD,AC的平行线,相交于点E.若AD=6,则点E到AB的距离是9.
如图,矩形ABCD的对角线AC,BD相交于点O,分别过点C,D作BD,AC的平行线,相交于点E.若AD=6,则点E到AB的距离是9. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.
如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.