题目内容
19.不等式组$\left\{\begin{array}{l}{1-x>0}\\{3x-5≤1}\end{array}\right.$的解集在数轴上表示正确的是( )| A. | 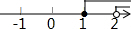 | B. | 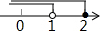 | C. | 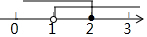 | D. | 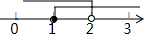 |
分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式1-x>0,得:x<1,
解不等式3x-5≤1,得:x≤2,
则不等式组的解集为x<1,
故选:B.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9.若圆锥的母线长是12,侧面展开图的圆心角是120°,则它的底面圆的半径为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
9.某大型商场进了一批成本为8元/件的儿童背心,调查发现,这种背心每周的销售量y(件)与它的定价x(元/件)的关系如下表;(x取整数)
(1)求这种儿童背心每周的销售量y(件)与它的定价x(元/件)之间的函数关系式(不必写出自变量x取值范围);
(2)为使商场每周获得最大利润,试问这种背心定价应为多少?最大利利润是多少?
(3)若商场每周想要获得不低于1050元的利润,试确定这种儿童背心的定价x(元/件)的取值范围.
| x(元/件) | 10 | 12 | 14 | 16 |
| y(件) | 200 | 180 | 160 | 140 |
(2)为使商场每周获得最大利润,试问这种背心定价应为多少?最大利利润是多少?
(3)若商场每周想要获得不低于1050元的利润,试确定这种儿童背心的定价x(元/件)的取值范围.
 如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.
如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.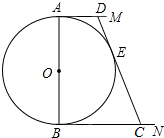 如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.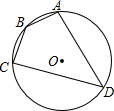 如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.
如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.