题目内容
1. 如图,在△ABC中,BI平分∠ABC,CI平分∠ACB,∠BIC=130°,则∠A=80°.
如图,在△ABC中,BI平分∠ABC,CI平分∠ACB,∠BIC=130°,则∠A=80°.
分析 首先根据BI平分∠ABC,CI平分∠ACB,推得∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB);然后根据三角形的内角和定理,求出∠IBC、∠ICB的度数和,进而求出∠A的度数是多少即可.
解答 解:∵BI平分∠ABC,CI平分∠ACB,
∴∠IBC=$\frac{1}{2}∠ABC$,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠BIC=130°,
∴∠IBC+∠ICB=180°-130°=50°,
∴∠ABC+∠ACB=50°×2=100°,
∴∠A=180°-100°=80°.
故答案为:80°.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的平分线把这个角分成两个大小相同的角.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
12.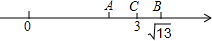 如图,数轴上表示3、$\sqrt{13}$的对应点分别为C、B,点C是AB的中点,则点A表示的数是( )
如图,数轴上表示3、$\sqrt{13}$的对应点分别为C、B,点C是AB的中点,则点A表示的数是( )
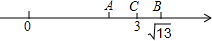 如图,数轴上表示3、$\sqrt{13}$的对应点分别为C、B,点C是AB的中点,则点A表示的数是( )
如图,数轴上表示3、$\sqrt{13}$的对应点分别为C、B,点C是AB的中点,则点A表示的数是( )| A. | 6-$\sqrt{13}$ | B. | 3-$\sqrt{13}$ | C. | $\sqrt{13}$-3 | D. | -$\sqrt{13}$ |
 如图,在△ABC中,AC的垂直平分线DE交AB于E,∠A=30°,∠ACB=70°,则∠BCE等于40°.
如图,在△ABC中,AC的垂直平分线DE交AB于E,∠A=30°,∠ACB=70°,则∠BCE等于40°.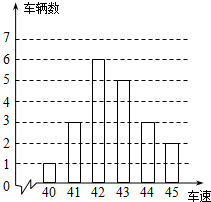 如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).
如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).