题目内容
10.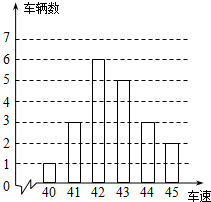 如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).
如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).(1)车速的众数是42千米/时,中位数是42.5千米/时;
(2)计算这些车辆的平均速度;
(3)若某天交警在该路口统计到该时段来往的车辆共1000辆,请估计车速大于43千米/时的有多少辆车?
分析 (1)根据众数的定义,找出车速的车辆数最多的即为众数,先求出车辆数的总数,再根据中位数的定义解答;
(2)根据加权平均数的计算方法列式计算即可得解;
(3)用1000乘以样本中车速大于43千米/时的车辆所占百分比即可.
解答 解:(1)该样本数据中车速是42千米/时的有6辆,最多,则该样本数据的众数为42千米/时,
样本容量为:1+3+6+5+3+2=20,按照车速从小到大的顺序排列,中位数是第10和11个数的平均数,
所以中位数是42和43的平均数,
(42+43)÷2=42.5(千米/时),
所以车速的中位数是42.5千米/时;
故答案为:42千米/时,42.5千米/时;
(2)这些车辆的平均速度是:
(40+41×3+42×6+43×5+44×3+45×2)÷20=42.6(千米/时).
答:这些车辆的平均数度是42.6千米/时;
(3)1000×$\frac{3+2}{20}$=250(辆).
即估计车速大于43千米/时的有250辆车.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,也考查了平均数、中位数、众数的定义以及用样本估计总体.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.方程3x-4y=2的一组解是( )
| A. | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=-7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
18.王刚今天到学校参加数学期末考试,从家里出发走10分钟到离家500米的地方吃早餐,吃早餐用了20分钟,再用10分钟赶到离家1000米的学校参加考试,下列图象中,能反应这一过程的是( )
| A. |  | B. | 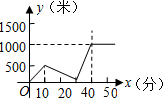 | ||
| C. | 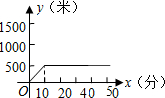 | D. |  |
20.下列方程中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}x+2y=0\\ 2x+y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=0}\\{y-x+5=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-2y-1=0\\-x=y+2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=4\\ 2x=z-2y\end{array}\right.$ |
 如图,在△ABC中,BI平分∠ABC,CI平分∠ACB,∠BIC=130°,则∠A=80°.
如图,在△ABC中,BI平分∠ABC,CI平分∠ACB,∠BIC=130°,则∠A=80°.
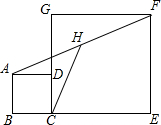 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=6,H是AF的中点,那么CH的长是2$\sqrt{5}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=6,H是AF的中点,那么CH的长是2$\sqrt{5}$.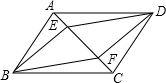 如图,在平行四边形ABCD中,对角线AC上有E、F两点,要使四边形BEDF是平行四边形,还需要增加一个条件是AE=CF.(填上一个即可).
如图,在平行四边形ABCD中,对角线AC上有E、F两点,要使四边形BEDF是平行四边形,还需要增加一个条件是AE=CF.(填上一个即可).