题目内容
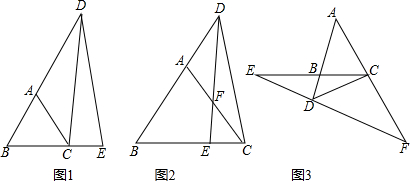
11. 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.
分析 根据点An的选法,罗列出部分点A的横坐标,根据点的变换即可发现变化规律“点An的横坐标为$(\sqrt{2})^{n-1}$×1=$(\sqrt{2})^{n-1}$”,根据这一规律即可找出A4的横坐标,再结合A、B之间的关系以及点Bn坐标的特征即可得出结论.
解答 解:观察,发现规律:点A1的横坐标为1,点A2的横坐标为$\sqrt{2}$×1,点A3的横坐标为$(\sqrt{2})^{2}$×1,…,
∴点An的横坐标为$(\sqrt{2})^{n-1}$×1=$(\sqrt{2})^{n-1}$,
∴点A4的横坐标为$(\sqrt{2})^{4-1}$=2$\sqrt{2}$,
∴点B4的横坐标为2$\sqrt{2}$.
又∵点Bn在直线y=x上,
∴点B4的纵坐标为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了一次函数图象上点的坐标特征以及规律型中的点的变换,解题的关键是发现规律“点An的横坐标为$(\sqrt{2})^{n-1}$×1=$(\sqrt{2})^{n-1}$”.本题属于基础题,难度不大,解决该题型题目时,根据一次函数图象上点的坐标特征找出点An的变化规律,根据变换规律即可得出结论.

练习册系列答案
相关题目
 如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.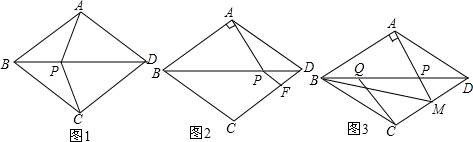 如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,
如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,