题目内容
12.我市部分学生参加了2007年全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:| 分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
| 人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
(1)全市共有300人参加本次数学竞赛决赛.
(2)决赛成绩分数的中位数落在60-79分数段内.
(3)经竞赛组委会评定,竞赛成绩在80分以上(含80分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例.
分析 (1)把频数分布表中各组的频数相加即可得到数据的总数;
(2)根据中位数的定义求解;
(3)用后三组的频数和除以总数即可得到参加本次竞赛决赛考生的获奖比例.
解答 解:(1)37+68+95+56+32+12=300(人).
所以全市共有300人参加本次数学竞赛决赛;
(2)第150个和151个数据都落在60-79分数段内,
所以决赛成绩分数的中位数落在60-79分数段内;
(3)$\frac{56+32+12}{300}$×100%=33.3%,
所以我市参加本次竞赛决赛考生的获奖比例为33.3%.
故答案为300,60-79.
点评 本题考查了频数分布表:在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.也考查了中位数.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
17.根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.17 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
2.一等腰三角形底边长为8cm,腰长为5cm,则腰上的高为( )
| A. | 3cm | B. | $\frac{5}{4}$cm | C. | $\frac{24}{5}$cm | D. | $\frac{12}{5}$cm |
 如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?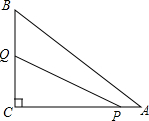 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).