��Ŀ����
1����ͼ����Rt��ABC �У�AC=4cm��BC=3cm����P��B������BA�ķ������A�����˶����ٶ�Ϊ1cm/s��ͬʱ��Q�� A������AC�ķ������C�����˶����ٶ�Ϊ2cm/s������PQ�����˶���ʱ��Ϊt��s��������0��t��2������������⣺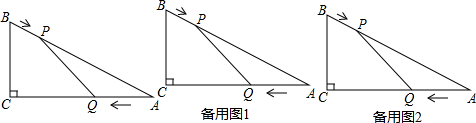
��1����tΪ��ֵʱ����P��Q��AΪ��������������ABC���ƣ�
��2���Ƿ����ijһʱ��t���߶�PQ����ABC������ֳ�1��2�����֣������ڣ������ʱ��t���������ڣ���˵�����ɣ�
��3����P��Q���˶��Ĺ����У���CPQ�ܷ��Ϊ���������Σ����ܣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
���� ��1���������������PQA�ס�BCA�͡�PQA�ס�CBA���������������ε������г�����ʽ��������㼴�ɣ�
��2�����S��APQ�����������г����̣��ⷽ�̼��ɣ�
��3�������������PC=PQ��CP=CQ��QP=QC�����ݵ��������ε����ʣ��������������ε����ʺ��ɶ�����ü��ɣ�
��� �⣺��1������ͼ1����PQA�ס�BCAʱ��
$\frac{5-t}{5}$=$\frac{2t}{4}$�����t=$\frac{10}{7}$��
����ͼ2����PQA�ס�CBAʱ��
$\frac{5-t}{4}$=$\frac{2t}{5}$�����t=$\frac{25}{13}$��
�֡�0��t��2��
��t=$\frac{10}{7}$��$\frac{25}{13}$��
��2����ͼ3������P��PH��CA������Ϊ��H��
���PHA�ס�BCA��
��$\frac{5-t}{5}$=$\frac{PH}{3}$��
��PH=$\frac{3}{5}$��5-t����
��S��APQ=$\frac{1}{2}$��2t��$\frac{3}{5}$��5-t��=-$\frac{3}{5}$t2+3t��
�߶�PQ����ABC������ֳ�1��2�����֣�
��S��APQ=$\frac{1}{3}$ S��ABC=$\frac{1}{3}$��6=2��S��APQ=$\frac{2}{3}$ S��ABC=$\frac{2}{3}$��6=4��
����-$\frac{3}{5}$t2+3t=2��-$\frac{3}{5}$t2+3t=4��
-$\frac{3}{5}$t2+3t=2ʱ�������ã�3t2-15t+10=0��
t1=$\frac{15+\sqrt{105}}{6}$ ����ȥ����t1=$\frac{15+\sqrt{105}}{6}$��2����t2=$\frac{15-\sqrt{105}}{6}$��
��t=$\frac{15-\sqrt{105}}{6}$��
-$\frac{3}{5}$t2+3t=4ʱ�������ã�3t2-15t+20=0��
�ߡ���0��
��t�⣮
��t=$\frac{15-\sqrt{105}}{6}$��
��3������ͼ4����PC=PQʱ������P��PG��CA��
����Ϊ��H�������ߺ�һ��֪��HQ=2-t��
�֡ߡ�PHA�ס�BCAʱ��
$\frac{5-t}{5}$=$\frac{2t+��2-t��}{4}$��
��t=$\frac{10}{9}$��
����ͼ5����CP=CQʱ������P��PM��CB������Ϊ��M��
�ɡ�BMP�ס�BCA��֪��BM=$\frac{3}{5}$t��MP=$\frac{4}{5}$t��
��CM=3-$\frac{3}{5}$t��
��Rt��PMC �У��ɹ��ɶ����ã���$\frac{4}{5}$t��2+��3-$\frac{3}{5}$t��2=��4-2t��2��
�����ã�15t2-62t+35=0��
���t=$\frac{31��2\sqrt{109}}{15}$��
��t1=$\frac{31+2\sqrt{109}}{15}$��t2=$\frac{31-2\sqrt{109}}{15}$��
��t1=$\frac{31+2\sqrt{109}}{15}$��2��
��t1=$\frac{31+2\sqrt{109}}{15}$ ����ȥ����
��t=$\frac{31-2\sqrt{109}}{15}$��
����ͼ6����QP=QCʱ������Q��QN��AB������Ϊ��N��
�ɡ�AQN�ס�ABC��֪��NQ=$\frac{6}{5}$t��NA=$\frac{8}{5}$t��
��PN=5-t-$\frac{8}{5}$t=5-$\frac{13}{5}$t��
��Rt��QNP �У��ɹ��ɶ����ã���$\frac{6}{5}$t��2+��5-$\frac{13}{5}$t��2=��4-2t��2��
�����ã�21t2-50t+45=0��
�ߡ�=-1280��0��
����⣬
�൱t=$\frac{10}{9}$��t=$\frac{31-2\sqrt{109}}{15}$ʱ����CPQ�ǵ��������Σ�
���� ���⿼��������������ε��ж������ʵ��ۺ����ã���ȷ���������ߡ�������ö����ǽ���Ĺؼ���ע����������˼���Ӧ�ã�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| ������ | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
| ���� | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
��1��ȫ�й���300�˲μӱ�����ѧ����������
��2�������ɼ���������λ������60-79�������ڣ�
��3����������ί�������������ɼ���80�����ϣ���80�֣��Ŀ������ɻ�ò�ͬ�ȼ��Ľ����������вμӱ��ξ������������Ļ�����
 ��ͼ���߳�Ϊ��m+3����������ֽƬ����һ���߳�Ϊm��������֮��ʣ�ಿ���ּ�ƴ��һ�������Σ����ص���϶������ƴ�ɵij�����һ�߳�Ϊ3�����ܳ��ǣ�������
��ͼ���߳�Ϊ��m+3����������ֽƬ����һ���߳�Ϊm��������֮��ʣ�ಿ���ּ�ƴ��һ�������Σ����ص���϶������ƴ�ɵij�����һ�߳�Ϊ3�����ܳ��ǣ�������| A�� | 2m+6 | B�� | 4m+12 | C�� | 2m+3 | D�� | m+6 |
| A�� | 4 | B�� | 6 | C�� | 4��6 | D�� | 8 |
 ��ͼ��ʾ����һ����Ϊ80cm����Ϊ50cm�ľ��η羰����������һ����ͬ���ȵĽ�ɫֽ�ߣ��Ƴ�һ�����ι�ͼ�����Ҫʹ������ͼ�������5400cm2�����ɫֽ�ߵĿ�Ϊxcm��������Ϳ����Ƕ��٣�
��ͼ��ʾ����һ����Ϊ80cm����Ϊ50cm�ľ��η羰����������һ����ͬ���ȵĽ�ɫֽ�ߣ��Ƴ�һ�����ι�ͼ�����Ҫʹ������ͼ�������5400cm2�����ɫֽ�ߵĿ�Ϊxcm��������Ϳ����Ƕ��٣�