题目内容
17.根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )| x | 6.17 | 6.18 | 6.19 | 6.20 |
| ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.17 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
分析 根据二次函数的增减性,可得答案.
解答 解:由y=ax2+bx+c,得x>6.17时y随x的增大而增大,得
x=6.18时,y=-0.01,x=6.19时,y=0.02,
ax2+bx+c=0的近似根是6.17<x<6.19,
故选:C.
点评 本题考查了估算一元二次方程的近似解,利用函数的增减性是解题关键.

练习册系列答案
相关题目
12.我市部分学生参加了2007年全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
请根据以上信息解答下列问题:
(1)全市共有300人参加本次数学竞赛决赛.
(2)决赛成绩分数的中位数落在60-79分数段内.
(3)经竞赛组委会评定,竞赛成绩在80分以上(含80分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例.
| 分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
| 人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
(1)全市共有300人参加本次数学竞赛决赛.
(2)决赛成绩分数的中位数落在60-79分数段内.
(3)经竞赛组委会评定,竞赛成绩在80分以上(含80分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例.
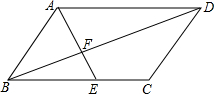 如图,在平行四边形ABCD中,BE:EC=2:1,AE与BD相交于点F,则BF:FD的值为$\frac{2}{3}$.
如图,在平行四边形ABCD中,BE:EC=2:1,AE与BD相交于点F,则BF:FD的值为$\frac{2}{3}$.
 如图所示的几何体是由5个相同的正方体搭成的,请画出这个几何体的正面看、左面看、上面看的形状图.
如图所示的几何体是由5个相同的正方体搭成的,请画出这个几何体的正面看、左面看、上面看的形状图.