题目内容
3. 如图,在△ABC中,∠C=90°,AB=10cm,AC=8cm.点P从点C出发沿CB以1cm/s的速度向终点B匀速运动;同时点Q从点A出发沿AB以acm/s的速度向点B匀速运动,以点C为圆心,CP为长为半径画⊙C交AC于点D,连接PQ、DQ、PD.若在运动的过程中PQ与⊙C始终保持相切,设运动时间为ts.
如图,在△ABC中,∠C=90°,AB=10cm,AC=8cm.点P从点C出发沿CB以1cm/s的速度向终点B匀速运动;同时点Q从点A出发沿AB以acm/s的速度向点B匀速运动,以点C为圆心,CP为长为半径画⊙C交AC于点D,连接PQ、DQ、PD.若在运动的过程中PQ与⊙C始终保持相切,设运动时间为ts.(1)a=$\frac{5}{3}$;
(2)当S△PQD=$\frac{2}{9}$S△ABC时,求t的值;
(3)是否存在t的值,使得△PQD是直角三角形?若存在,求出t的值;若不存在,说明理由.
分析 (1)如图1中,作QM⊥AC于M.首先证明四边形PCMQ是矩形,由QM∥BC,得$\frac{QM}{BC}$=$\frac{AQ}{AB}$,可得方程$\frac{t}{6}$=$\frac{at}{10}$,解方程即可.
(2)由PQ∥AC,得$\frac{PQ}{AC}$=$\frac{BP}{BC}$,即$\frac{PQ}{8}$=$\frac{6-t}{6}$,推出PQ=$\frac{4}{3}$(6-t),根据S△PQD=$\frac{2}{9}$S△ABC,列出方程,解方程即可.
(3)分两种情形讨论)①当∠PDQ=90°,易知△PDQ是等腰直角三角形,则有$\frac{1}{2}$PQ=PC,②当∠PQD=90°时,则有AM+CD=8,分别构建方程解决问题.
解答 解:(1)如图1中,作QM⊥AC于M.
在Rt△ABC中,∵AB=10,AC=8,
BC=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵PQ是⊙C的切线,
∴PQ⊥BC,
∴∠QPC=∠PCM=∠CMQ=90°,
∴四边形PCMQ是矩形,
∴QM=PC=t,
∵QM∥BC,
∴$\frac{QM}{BC}$=$\frac{AQ}{AB}$
∴$\frac{t}{6}$=$\frac{at}{10}$,
∴a=$\frac{5}{3}$cm/s.
故答案为$\frac{5}{3}$.
(2)∵PQ∥AC,
∴$\frac{PQ}{AC}$=$\frac{BP}{BC}$,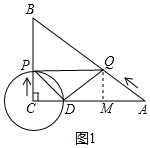
∴$\frac{PQ}{8}$=$\frac{6-t}{6}$,
∴PQ=$\frac{4}{3}$(6-t),
∵S△PQD=$\frac{2}{9}$S△ABC,
∴$\frac{1}{2}$•$\frac{4}{3}$(6-t)•t=$\frac{2}{9}$•$\frac{1}{2}$•6•8,
∴t=2或4.
(3)①当∠PDQ=90°,易知△PDQ是等腰直角三角形,则有$\frac{1}{2}$PQ=PC,
∴$\frac{4}{3}$(6-t)=2t,
∴t=$\frac{12}{5}$.
②当∠PQD=90°时,则有AM+CD=8,
∴$\frac{4}{3}$t+t=8,
∴t=$\frac{24}{7}$,
综上所述,t=$\frac{18}{11}$s或$\frac{24}{7}$s时,△PQD是直角三角形.
点评 本题考查圆综合题、矩形的判定和性质、平行线分线段成比例定理、三角形的面积等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会把问题转化为方程解决,属于中考压轴题.

| A. | 调查全国初中生的身体素质情况 | |
| B. | 调查一批蜡烛的使用寿命 | |
| C. | 调查一架“歼20”隐形战机各部零件的质量 | |
| D. | 调查我国2012年中央电视台春节联欢晚会的收视率 |
| A. | m=1 | B. | m=-1 | C. | m=2 | D. | m无法求出 |
-0.333…,$\sqrt{4}$,$\sqrt{5}$,-π,3π,3.1415.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
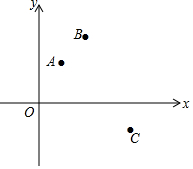 如图7,在平面直角坐标系中,已知某个二次函数的图象经过点A(1,m),B(2,n),C(4,t),且点B是该二次函数图象的顶点.请在图7中描出该函数图象上另外的两个点,并画出图象.
如图7,在平面直角坐标系中,已知某个二次函数的图象经过点A(1,m),B(2,n),C(4,t),且点B是该二次函数图象的顶点.请在图7中描出该函数图象上另外的两个点,并画出图象.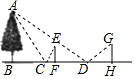 某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).
某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).