题目内容
小颖准备用21元钱买笔和笔记本．已知每枝笔3元，每个笔记本2.2元，她买了2个笔记本．请你帮她算一算，她还可能买几枝笔？
她还可能买5枝笔．
【解析】【试题分析】设她还可能买x只笔，根据总钱数不超过21元，列不等式求解．
【试题解析】设她还可能买x只笔，
由题意得，3x+2×2.2≤21，
解得：x≤．
答：她还可能买5枝笔．
___________
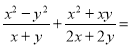【解析】试题分析：原式＝
＝
＝．
故答案为． 若
x2m－1－8＞5是一元一次不等式，则m的值为( )
A. 0 B. 1
C. 2 D. 3
B
【解析】根据一元一次不等式的定义得： ，故选B. 甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．
（1）根据题意，填写下表（单位：元）；
累计购物 实际花费 | 130 | 290 | … | x |
在甲商场 | 127 |
| … |
|
在乙商场 | 126 |
| … |
|
（2）当x取何值时，小红在甲、乙两商场的实际花费相同？
（3）当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？
（1）在甲商场：100+（290﹣100）×0.9=271，100+（x﹣100）×0.9=0.9x+10；
在乙商场：50+（290﹣50）×0.95=278，50+（x﹣50）×0.95=0.95x+2.5；
（2）当x为150时，小红在甲、乙两商场的实际花费相同；
（3）当小红累计购物超过100元而不到150元时，在乙商场实际花费少；正好为150元时，两商场花费相同；大于1... 小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3（2x-100）＜1000，则下列何者可能是小美告诉小明的内容？（ ）
A. 买两件等值的商品可减100元，再打3折，最后不到1000元
B. 买两件等值的商品可减100元，再打7折，最后不到1000元
C. 买两件等值的商品可打3折，再减100元，最后不到1000元
D. 买两件等值的商品可打7折，再减100元，最后不到1000元
A
【解析】【解析】
由关系式可知：
0.3（2x﹣100）＜1000，
由2x﹣100，得出两件商品减100元，以及由0.3（2x﹣100）得出买两件打3折，
故可以理解为：买两件等值的商品可减100元，再打3折，最后不到1000元．
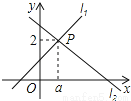
故选A． 直线l1：y=x+1与直线l2：y=mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为 ．
x≥1
【解析】
试题分析：首先把P（a，2）坐标代入直线y=x+1，求出a的值，从而得到P点坐标，再根据函数图象可得答案．
【解析】
将点P（a，2）坐标代入直线y=x+1，得a=1，
从图中直接看出，当x≥1时，x+1≥mx+n，
故答案为：x≥1． 不等式组﹣1＜x＜4的整数解有_________个．
4
【解析】在﹣1＜x＜4范围内的整数只有0，1，2，3，
所以等式﹣1＜x＜4的整数解有4个，
故答案为4． 如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
（1）证明见解析；（2）6．
【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
试题解析：（1）∵D、G分别是AB、AC的中点，... 如图，在?ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于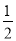
EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（ ）
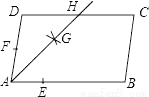
A. AG平分∠DAB B. AD=DH C. DH=BC D. CH=DH
D
【解析】试题分析：由角平分线的作法，依题意可知AG平分∠DAB，A正确；∠DAH＝∠BAH，又AB∥DC，所以∠BAH＝∠ADH，所以，∠DAH＝∠ADH，所以，AD＝DH，又AD＝BC，所以，DH＝BC，B、C正确，故答案选D.