题目内容
小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3（2x-100）＜1000，则下列何者可能是小美告诉小明的内容？（ ）
A. 买两件等值的商品可减100元，再打3折，最后不到1000元
B. 买两件等值的商品可减100元，再打7折，最后不到1000元
C. 买两件等值的商品可打3折，再减100元，最后不到1000元
D. 买两件等值的商品可打7折，再减100元，最后不到1000元
A
【解析】【解析】
由关系式可知：
0.3（2x﹣100）＜1000，
由2x﹣100，得出两件商品减100元，以及由0.3（2x﹣100）得出买两件打3折，
故可以理解为：买两件等值的商品可减100元，再打3折，最后不到1000元．
故选A．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
计算：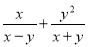 
，其中x=1，y=2.
【解析】试题分析：先通分，再相加，化简后代入x、y的值计算即可．
试题解析：
原式＝
＝，
当x＝1、y＝2时，
原式＝
＝． 按要求解答下列各题：
(1)解不等式：3x－5＜2(2＋3x)；
(2)解不等式：2x－3≤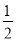
(x＋2)；
(3)解不等式： 
＜x－1，并将解集在数轴上表示出来．
(1)x＞－3 (2)x≤ (3)x＞2，画数轴略
【解析】【试题分析】（1）去括号得： 移项得： 合并同类项得： 系数化为1得：x＞－3 ；
(2) 去括号得： 移项得： 合并同类项得： 系数化为1得： x≤ ；
(3)去分母得： 移项得： ，合并得： 系数化为1得：x＞2，数轴见解析.
【试题解析】
去括号得：
移项得：
合并同类项得：
系数化为... 如图，AD平分∠BAC，AB=AC，那么判定△ABD≌△ACD的理由是（ ）
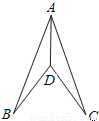
A. SSS B. SAS C. ASA D. AAS
B
【解析】∵AD平分∠BAC，
∴∠BAD=∠CAD，
又∵AB=AC，AD=AD，
∴可由“SAS”判定△ABD≌△ACD.
故选B. 有3人携带会议材料乘坐电梯，这三人的体重共210 kg，每捆材料重20 kg，电梯最大负荷为1 050 kg，则该电梯在此3人乘坐的情况下最多还能搭载_______捆材料．
42
【解析】(1050-210) 小颖准备用21元钱买笔和笔记本．已知每枝笔3元，每个笔记本2.2元，她买了2个笔记本．请你帮她算一算，她还可能买几枝笔？
她还可能买5枝笔．
【解析】【试题分析】设她还可能买x只笔，根据总钱数不超过21元，列不等式求解．
【试题解析】设她还可能买x只笔，
由题意得，3x+2×2.2≤21，
解得：x≤．
答：她还可能买5枝笔． 一次函数y=﹣3x+12中x_________ 时，y＜0．
＞4
【解析】根据题意得：﹣3x+12＜0，
解得：x＞4．
故答案为：＞4； 下列不等式一定成立的是（ ）
A. 5a＞4a B. x+2＜x+3 C. ﹣a＞﹣2a D.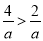 
B
【解析】A、因为5＞4，不等式两边同乘以a，而a≤0时，不等号方向改变，即5a≤4a，故错误；B、因为2＜3，不等式两边同时加上x，不等号方向不变，即x+2＜x+3正确；
C、因为﹣1＞﹣2，不等式两边同乘以a，而a≤0时，不等号方向改变，即﹣a≤﹣2a，故错误；
D、因为4＞2，不等式两边同除以a，而a≤0时，不等号方向改变，即，故错误．
故选B． 如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D1，折痕为EF，若∠BAE=55°，则∠D1AD=__．
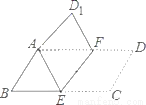
55°．
【解析】试题分析：已知四边形ABCD是平行四边形，由平行四边形的性质可得∠BAD=∠C，再由折叠的性质得∠D1AE=∠C，所以∠D1AE=∠BAD，即可得∠D1AD=∠BAE=55°；