题目内容
9.在等腰△ABC中,AB=AC,cos∠ABC$\frac{4}{5}$,点P是直线BC上一点,且PC PB=1:3,则tan∠APB=$\frac{3}{2}$或$\frac{3}{8}$.分析 如图,过D作AD⊥BC于D,根据等腰三角形的性质得到BD=CD,根据cos∠ABC=$\frac{4}{5}$,设BD=4x,AB=5x,得到BC=8x,由于PC:PB=1:3,得到PD=2x,根据三角函数的定义即可得到结论.
解答 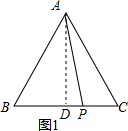 解:如图1,过D作AD⊥BC于D,∵AB=AC,
解:如图1,过D作AD⊥BC于D,∵AB=AC,
∴BD=CD,
∵cos∠ABC=$\frac{4}{5}$,
∴设BD=4x,AB=5x,
∴AD=3x,
∴BC=8x,
∵PC:PB=1:3,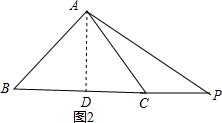
∴PB=6x,
∴PD=2x,
∴tan∠APB=$\frac{AD}{PD}=\frac{3x}{2x}$=$\frac{3}{2}$;
如图2,∵PC:PB=1:3,
∴PB=12x,
∴PD=8x,
∴tan∠APB=$\frac{AD}{PD}=\frac{3x}{2x}$$\frac{AD}{PD}=\frac{3x}{8x}$=$\frac{3}{8}$;
综上所述:tan∠APB=$\frac{3}{2}$或$\frac{3}{8}$.
故答案为:$\frac{3}{2}$或$\frac{3}{8}$.
点评 本题考查了解直角三角形,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8. 如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
 如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
20.成成在满分为100分的期中、期末数学测试中,两次的平均分为90分,若按期中数学成绩占30%,期末数学成绩占70%计算学期数学成绩,则成成的学期数学成绩可能是( )
| A. | 85 | B. | 88 | C. | 95 | D. | 100 |
14.下列运算正确的是( )
| A. | a2•a3=a6 | B. | ($\frac{1}{2}$)-1=-2 | C. | |-6|=6 | D. | $\sqrt{16}$=±4 |
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: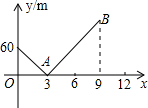 小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题: 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=4,DB=5,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=4,DB=5,求阴影部分的面积.