题目内容
14.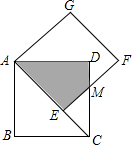 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )| A. | -4+4$\sqrt{2}$ | B. | 4$\sqrt{2}$+4 | C. | 8-4$\sqrt{2}$ | D. | $\sqrt{2}$+1 |
分析 阴影部分的面积=S△ACD-S△MEC,△ACD和△MEC都是等腰直角三角形,利用面积公式即可求解.
解答 解:∵四边形ABCD是正方形,
∴∠D=90°,∠ACD=45°,AD=CD=2,
则S△ACD=$\frac{1}{2}$AD•CD=$\frac{1}{2}$×2×2=2;
AC=$\sqrt{2}$AD=2$\sqrt{2}$,
则EC=2$\sqrt{2}$-2,
∵△MEC是等腰直角三角形,
∴S△MEC=$\frac{1}{2}$ME•EC=$\frac{1}{2}$(2$\sqrt{2}$-2)2=6-4$\sqrt{2}$,
∴阴影部分的面积=S△ACD-S△MEC=2-(6-4$\sqrt{2}$)=4$\sqrt{2}$-4.
故选:A.
点评 本题考查了正方形的性质,等腰直角三角形的性质;注意到阴影部分的面积=S△ACD-S△MEC是关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | a3•a2=a6 | B. | $\sqrt{9}$=3 | C. | (a2)3=a5 | D. | 4a-2a=2 |
6.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | a6÷a2=a3 | C. | (π-3)0=1 | D. | (2a)3=6a3 |
3.下列运算结果为负数的是( )
| A. | -(-2) | B. | (-2)2 | C. | |-2| | D. | (-2)3 |
4.下列计算正确的是( )
| A. | a4÷a3=1 | B. | a4+a3=a7 | C. | (2a3)4=8a12 | D. | a4•a3=a7 |
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: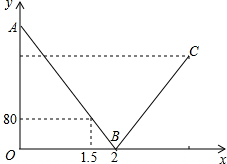 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题: 在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.
在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°. 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=4,DB=5,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=4,DB=5,求阴影部分的面积.