题目内容
15.探索与发现:(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是a1⊥a3,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是a1∥a4(直接填结论,不需要说明理由)
(3)现在有2014条直线a1,a2,a3,…,a2014,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2014的位置关系.
分析 (1)根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答;
(2)根据(1)中结论即可判定垂直;
(3)根据观察发现规律,以四次为一个循环,⊥,⊥,∥,∥,根据此规律即可解决问题.
解答 解:(1)a1⊥a3.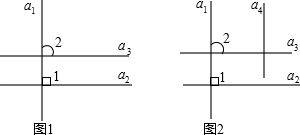
理由如下:如图1,∵a1⊥a2,
∴∠1=90°,
∵a2∥a3,
∴∠2=∠1=90°,
∴a1⊥a3;
故答案为a1⊥a3.
(2)同(1)的解法,如图2,直线a1与a4的位置关系是:a1∥a4;
故答案为a1∥a4.
(3)∵a1⊥a2,a1⊥a3,a1∥a4,a1∥a5…
以四次为一个循环,⊥,⊥,∥,∥
规律:下标除以4余数为2或3垂直,下标除以4余数为0或1平行,
2014÷4的余数为2,
∴a1⊥a2014,
所以直线a1与a2014的位置关系是:a1⊥a2014.
点评 本题考查了平行线的判定、规律探究题目,解题的关键是发现规律,以四次为一个循环,⊥,⊥,∥,∥,属于中考填空压轴题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.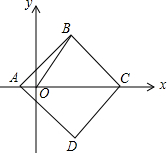 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
3.校办工厂要制作一些等腰三角形模具,工人师傅对四个模具的尺寸按照底边、腰长和底边上的高的顺序进行了记录,其中记录错误的是( )
| A. | 10,26,24 | B. | 16,10,6 | C. | 30,17,8 | D. | 24,13,5 |
20.成成在满分为100分的期中、期末数学测试中,两次的平均分为90分,若按期中数学成绩占30%,期末数学成绩占70%计算学期数学成绩,则成成的学期数学成绩可能是( )
| A. | 85 | B. | 88 | C. | 95 | D. | 100 |
5.下列运算正确的是( )
| A. | a3•a2=a6 | B. | $\sqrt{9}$=3 | C. | (a2)3=a5 | D. | 4a-2a=2 |
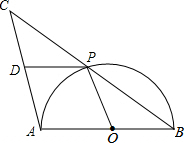 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
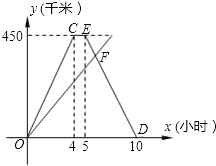 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: