题目内容
16.一次函数y=(m+2)x+3-m,若y随x的增大而增大,函数图象与y轴的交点在x轴的上方,则m的取值范围是-2<m<3.分析 由一次函数为增函数可得出k=m+2>0,再由函数图象与y轴的交点在x轴的上方可得出b=3-m>0,联立成不等式组,解不等式组即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{m+2>0}\\{3-m>0}\end{array}\right.$,
解得:-2<m<3.
故答案为:-2<m<3.
点评 本题考查了一次函数的性质,解题的关键是根据已知得出关于m的不等式组.本题属于基础题,难度不大,解决该题型题目时,根据一次函数的性质结合题意得出关于一次函数系数的不等式(不等式组)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列运算正确的是( )
| A. | (3x2)3=9x6 | B. | a6÷a2=a3 | C. | (a+b)2=a2+b2 | D. | (a-b)(a+b)=a2-b2 |
8. 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
5.下列运算正确的是( )
| A. | a3•a2=a6 | B. | $\sqrt{9}$=3 | C. | (a2)3=a5 | D. | 4a-2a=2 |
6.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | a6÷a2=a3 | C. | (π-3)0=1 | D. | (2a)3=6a3 |
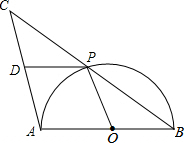 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.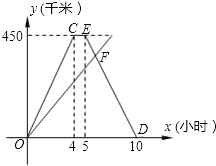 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: