题目内容
9．下列四组线段中，不能组成直角三角形的一组是（ ）| A． | 1，1，$\sqrt{2}$ | B． | 1，2，$\sqrt{3}$ | C． | 2.1，2.8，3.4 | D． | 9，12，15 |
分析 根据勾股定理的逆定理进行计算，判断即可．
解答 解：12+12=（$\sqrt{2}$）2，A能组成直角三角形；
12+（$\sqrt{3}$）2=22，B能组成直角三角形；
2.12+2.82≠3.42，C不能组成直角三角形；
92+122=152，D能组成直角三角形；
故选：C．
点评 本题考查的是勾股定理的逆定理的应用，如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
相关题目
19．
如图，点A，B在数轴上，以AB为边作正方形，该正方形的面积为8，若点A对应的数是-2，则B对应的数是（ ）
如图，点A，B在数轴上，以AB为边作正方形，该正方形的面积为8，若点A对应的数是-2，则B对应的数是（ ）| A． | 2$\sqrt{2}$-2 | B． | 2-2$\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | 2$\sqrt{2}$+2 |
17．
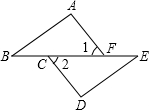已知点B、C、F、E共线，∠1=∠2，AF=CD，要使△ABF≌△DEC，还需要补充一个条件，下列选项中不能满足要求的是（ ）
已知点B、C、F、E共线，∠1=∠2，AF=CD，要使△ABF≌△DEC，还需要补充一个条件，下列选项中不能满足要求的是（ ）| A． | AB=DE | B． | ∠A=∠D | C． | AB∥DE | D． | BC=EF |
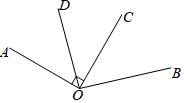如图，OA⊥OC，∠BOC=50°，若OD平分∠AOC，则∠BOD=95°．
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上．