题目内容
12.为了2010年世博会,上海市准备对黄浦江边的某工程进行改造.若请甲工程队单独做此项工程需3个月完成,每月耗资12万元;若请乙工程队单独做此项工程需6个月完成,每月耗资5万元.(1)请问甲、乙两工程队合作需几个月完成?耗资多少万元?
(2)因其它原因,要求最迟4个月完成此项工程即可,请你设计一种方案,既保证完成任务,又最大限度节省资金.(时间按整数月计算)
分析 (1)把工作总量看作单位“1”,先分别求出甲、乙的工作效率,再求出合作的工作效率,最后用工作总量除以合作的工作效率,就是合作的工作时间;再根据甲、乙做此工程的耗资的钱数,求出合作时的耗资钱数;
(2)甲,乙合做一段时间,剩下的乙来做,就可以既保证完成任务,又最大限度节省资金.
解答 解:(1)1÷(1÷3+1÷6),
=1÷($\frac{1}{3}$+$\frac{1}{6}$),
=1$÷\frac{1}{2}$,
=2(月),
2×(12+5)=34(万元),
(2)设甲乙合做x个月,剩下的由乙来完成.
($\frac{1}{3}$+$\frac{1}{6}$)x+$\frac{4-x}{6}$=1,
$\frac{1}{2}$x+$\frac{4-x}{6}$=1,
3x+4-x=6,
2x=2,
x=1
所以甲乙合作一个月,剩下的由乙来做3个月就可以.
点评 此题主要考查了工作时间、工作效率、工作总量三者之间的数量关系,解答时往往把工作总量看作“1”,再利用它们的数量关系解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.不等式2y-1<-3的解集是( )
| A. | x>-1 | B. | x<-1 | C. | y>-1 | D. | y<-1 |
9.下列四组线段中,不能组成直角三角形的一组是( )
| A. | 1,1,$\sqrt{2}$ | B. | 1,2,$\sqrt{3}$ | C. | 2.1,2.8,3.4 | D. | 9,12,15 |
6.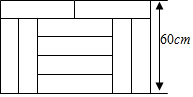 如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
 如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )
如图,宽为60cm的矩形图案由10个完全一样的小长方形拼成,则其中一个小长方形的周长为( )| A. | 60cm | B. | 120cm | C. | 312cm | D. | 576cm |
4.在正整数中,1是( )
| A. | 最小的奇数 | B. | 最小的偶数 | C. | 最小的素数 | D. | 最小的合数 |
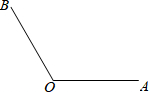 如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.
如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.