题目内容
14．
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上．（1）求△ABC的面积．
（2）求AB，AC的长分别是多少．
分析 （1）根据三角形的面积公式计算；
（2）根据勾股定理计算即可．
解答 解：（1）△ABC的面积=$\frac{1}{2}$×7×5=17.5；
（2）由勾股定理得，AB=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$，
AC=$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$．
点评 本题考查的是勾股定理的应用，直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
相关题目
4．下列运算正确的是（ ）
| A． | 3x2+2x3=5x6 | B． | （-x3）2=x6 | C． | 3-2=$\frac{1}{6}$ | D． | 50=0 |
5．将 3a2m-6amn+3a分解因式，下面是四位同学分解的结果：
①3am（a-2n+1）②3a（am+2mn-1）③3a（am-2mn） ④3a（am-2mn+1）
其中，正确的是（ ）
①3am（a-2n+1）②3a（am+2mn-1）③3a（am-2mn） ④3a（am-2mn+1）
其中，正确的是（ ）
| A． | ① | B． | ② | C． | ③ | D． | ④ |
9．下列四组线段中，不能组成直角三角形的一组是（ ）
| A． | 1，1，$\sqrt{2}$ | B． | 1，2，$\sqrt{3}$ | C． | 2.1，2.8，3.4 | D． | 9，12，15 |
19．
广州市某中学开展主题为“我爱阅读”的专题调查活动，了解学校1200名学生一年内阅读书籍的数量，随机抽取部分学生进行统计，绘制成如下尚未完成的频数分布表和频数分布直方图．请根据图表，解答下面的问题：
（1）a=0.32，b=6，c=0.12，d=50．
（2）补全频数分布直方图．
（3）根据该样本，估计该校学生阅读书籍数量在15本或以上的人数．
（4）如果阅读书籍数量在10本或以上的人数占总人数的70%以上，那么该校能评为“书香校园”，请根据上述数据分析该校是否能获得此荣誉，并说明理由．
广州市某中学开展主题为“我爱阅读”的专题调查活动，了解学校1200名学生一年内阅读书籍的数量，随机抽取部分学生进行统计，绘制成如下尚未完成的频数分布表和频数分布直方图．请根据图表，解答下面的问题：| 分组 | 频数 | 频率 |
| 0≤x＜5 | 4 | 0.08 |
| 5≤x＜10 | 14 | 0.28 |
| 10≤x＜15 | 16 | a |
| 15≤x＜20 | b | c |
| 20≤x＜25 | 10 | 0.2 |
| 合计 | d | 1.00 |
（2）补全频数分布直方图．
（3）根据该样本，估计该校学生阅读书籍数量在15本或以上的人数．
（4）如果阅读书籍数量在10本或以上的人数占总人数的70%以上，那么该校能评为“书香校园”，请根据上述数据分析该校是否能获得此荣誉，并说明理由．
6．
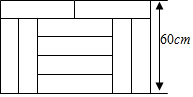如图，宽为60cm的矩形图案由10个完全一样的小长方形拼成，则其中一个小长方形的周长为（ ）
如图，宽为60cm的矩形图案由10个完全一样的小长方形拼成，则其中一个小长方形的周长为（ ）| A． | 60cm | B． | 120cm | C． | 312cm | D． | 576cm |