题目内容
20.已知点P(2m+4,m-1),请分别根据下列条件,求出点P的坐标.(1)点P在x轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过点A(2,-4)且与y轴平行的直线上.
分析 (1)根据x轴上点的纵坐标为0列方程求出m的值,再求解即可;
(2)根据纵坐标与横坐标的关系列方程求出m的值,再求解即可;
(3)根据平行于y轴的直线上的点的横坐标相同列方程求出m的值,再求解即可.
解答 解:(1)∵点P(2m+4,m-1)在x轴上,
∴m-1=0,
解得m=1,
∴2m+4=2×1+4=6,
m-1=0,
所以,点P的坐标为(6,0);
(2)∵点P(2m+4,m-1)的纵坐标比横坐标大3,
∴m-1-(2m+4)=3,
解得m=-8,
∴2m+4=2×(-8)+4=-12,
m-1=-8-1=-9,
∴点P的坐标为(-12,-9);
(3)∵点P(2m+4,m-1)在过点A(2,-4)且与y轴平行的直线上,
∴2m+4=2,
解得m=-1,
∴m-1=-1-1=-2,
∴点P的坐标为(2,-2).
点评 本题考查了点的坐标,熟练掌握坐标轴上点的坐标特征以及平行于坐标轴的直线上的点的坐标特征是解题的关键.

练习册系列答案
相关题目
10.可以用来说明命题“若|a|>0.5,则a>0.5”是假命题的反例( )
| A. | 可以是a=-1,也可以是a=1 | B. | 可以是a=1,不可以是a=-1 | ||
| C. | 可以是a=-1,不可以是a=1 | D. | 既不可以是a=-1,也不可以是a=1 |
8.不等式2y-1<-3的解集是( )
| A. | x>-1 | B. | x<-1 | C. | y>-1 | D. | y<-1 |
5.将 3a2m-6amn+3a分解因式,下面是四位同学分解的结果:
①3am(a-2n+1)②3a(am+2mn-1)③3a(am-2mn) ④3a(am-2mn+1)
其中,正确的是( )
①3am(a-2n+1)②3a(am+2mn-1)③3a(am-2mn) ④3a(am-2mn+1)
其中,正确的是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
9.下列四组线段中,不能组成直角三角形的一组是( )
| A. | 1,1,$\sqrt{2}$ | B. | 1,2,$\sqrt{3}$ | C. | 2.1,2.8,3.4 | D. | 9,12,15 |
4.在正整数中,1是( )
| A. | 最小的奇数 | B. | 最小的偶数 | C. | 最小的素数 | D. | 最小的合数 |
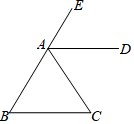 如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.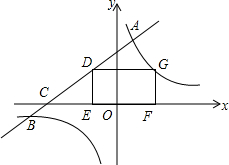 如图,已知直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的顶点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=1.5,CE=2,点A的横坐标是1.
如图,已知直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的顶点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=1.5,CE=2,点A的横坐标是1.