题目内容
5.规定一种新的运算:a△b=n,(a+c)△b=n-2c,a△(b+c)=n+c.且1△1=2,则2015△2015的值为2011.分析 a△b=n,(a+c)△b=n-2c,a△(b+c)=n+c表示当a增加c时,结果减少2c,当b增加c时,结果增加c,据此首先求得2015△1,然后求得2015△2015的值.
解答 解:∵1△1=2,
∴2015△1=(1+2014)△1=2-2×2014=-4026,
∴2015△2015=2015△(1+2014)=-4026+2015=-2011.
故答案是:2011.
点评 本题考查了有理数的混合运算,理解题目中规定的运算,理解a和b的变化与结果变化之间的关系是关键.

练习册系列答案
相关题目
15.已知方程7x-1=6x,则根据等式的性质,下列变形正确的有( )
①-1=7x+6x;
②$\frac{7}{2}$x-$\frac{1}{2}$=3x
③7x-6x-1=0;
④7x+6x=1.
①-1=7x+6x;
②$\frac{7}{2}$x-$\frac{1}{2}$=3x
③7x-6x-1=0;
④7x+6x=1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.方程11x+1=5(2x+1)的解是( )
| A. | 0 | B. | -6 | C. | 4 | D. | 6 |
17.平面内n(n≥2)条直线,每两条直线都相交,交点个数最多有( )
| A. | n | B. | n(n-1) | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n(n-1)}{2}$ |
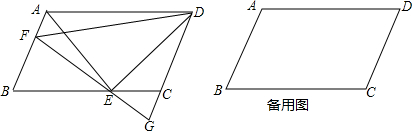
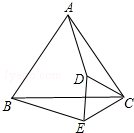 如图所示,已知:△ABC和△CDE都是等边三角形.求证:AD=BE.
如图所示,已知:△ABC和△CDE都是等边三角形.求证:AD=BE.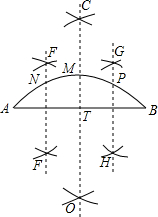 小明四等分弧AB,他的作法如下:
小明四等分弧AB,他的作法如下: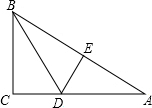 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.