题目内容
2.在x2□2x□1的空格中,任意填上“+”“-”,求其中能构成完全平方的概率(列出表格或画出树形图)分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与其中能构成完全平方的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有4种等可能的结果,其中能构成完全平方的有2种情况,
∴其中能构成完全平方的概率为:$\frac{2}{4}$=$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
17.平面内n(n≥2)条直线,每两条直线都相交,交点个数最多有( )
| A. | n | B. | n(n-1) | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n(n-1)}{2}$ |
12. 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
(1)请算出三人的民主评议得分;
(2)该单位将笔试,面试,民主评议三项测试得分按2:1:2的比例确定综合成绩,谁将被录用?请说明理由.
 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)| 测试项目 | 测试成绩分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 85 | 95 |
| 面试 | 98 | 75 | 73 |
(2)该单位将笔试,面试,民主评议三项测试得分按2:1:2的比例确定综合成绩,谁将被录用?请说明理由.
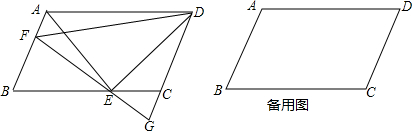
 如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为22cm.
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为22cm.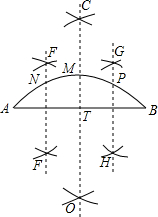 小明四等分弧AB,他的作法如下:
小明四等分弧AB,他的作法如下: