题目内容
20.已知:半圆O的直径AB=6,点C在半圆O上,且tan∠ABC=2$\sqrt{2}$,点D为弧AC上一点,联结DC(如图)(1)求BC的长;
(2)若射线DC交射线AB于点M,且△MBC与△MOC相似,求CD的长;
(3)联结OD,当OD∥BC时,作∠DOB的平分线交线段DC于点N,求ON的长.
分析 (1)如图1中,根据AB是直径,得△ABC是直角三角形,利用勾股定理即可解决问题.
(2)如图2中,只要证明△OBC≌△OCD得BC=CD,即可解决问题.
(3)如图3中,延长ON交BC的延长线于G,作GH⊥OB于H,先求出BG,根据tan∠HBG=2$\sqrt{2}$,利用勾股定理求出线段HB、HG,再利用CG∥DO得$\frac{CG}{OD}=\frac{GN}{ON}$,由此即可解决.
解答 解;(1)如图1中,连接AC,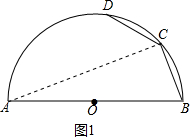
∵AB是直径,
∴∠ACB=90°,
∵tan∠ABC=2$\sqrt{2}$,
∴可以假设AC=2$\sqrt{2}$k,BC=k,
∵AB=6,AB2=AC2+BC2,
∴36=8k2+k2,
∴k2=4,
∵k>0,
∴k=2,BC=2.
(2)如图2中,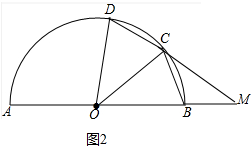
∵△MBC与△MOC相似,
∴∠MBC=∠MCO,
∵∠MBC+∠OBC=180°,∠MCO+∠OCD=180°,
∴∠OBC=∠OCD,
∵OB=OC=OD,
∴∠OBC=∠OCB=∠OCD=∠ODC,
在△OBC和△OCD中,
$\left\{\begin{array}{l}{∠OBC=∠OCD}\\{∠OCB=∠ODC}\\{OB=OC}\end{array}\right.$,
∴△OBC≌△OCD,
∴BC=CD=2.
(3)如图3中,延长ON交BC的延长线于G,作GH⊥OB于H.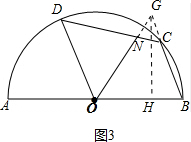
∵BC∥OD,
∴∠DOG=∠OGB=∠GOB,
∴BO=BG=3,
∵tan∠HBG=$\frac{GH}{HB}=2\sqrt{2}$,设GH=2$\sqrt{2}$a,HB=a,
∵BG2=GH2+HB2,
∴8a2+a2=9,
∴a2=1,
∵a>0,
∴a=1,HB=1,GH=2$\sqrt{2}$,OH=2,OG=$\sqrt{O{H}^{2}+H{G}^{2}}$=2$\sqrt{3}$,
∵GC∥DO,
∴$\frac{GN}{ON}=\frac{CG}{OD}$=$\frac{1}{3}$,
∴ON=$\frac{3}{4}$×$2\sqrt{3}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查圆的有关知识、全等三角形的判定和性质、相似三角形的性质、勾股定理等知识,灵活应用这些知识解决问题是解题的关键,第三个问题的关键是利用平行线分线段成比例定理,属于中考压轴题.

| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
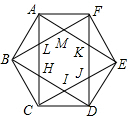 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )| A. | 18$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{18\sqrt{3}}{2}$ |
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.