题目内容
19．在平面直角坐标系xOy中，若抛物线y=ax2+bx+c的顶点为M，且经过A（0，4），B（4，4）两点，若M到线段AB的距离为4，则a=1或-1．
分析 根据题意求得顶点M的坐标，然后设出顶点式，根据待定系数法即可求得．
解答 解：∵A（0，4），B（4，4），
∴AB∥x轴，
∵M到线段AB的距离为4，
∴M（2，8）或（2，0），
①当M（2，8）时，设抛物线的解析式为y=a（x-2）2+8，
代入A（0，4）得，4=4a+8，
解得a=-1，
②当M（2，0）时，设抛物线的解析式为y=a（x-2）2，
代入A（0，4）得，4=4a，
解得a=1，所以a=1或-1，
故答案为1或-1．
点评 本题考查了二次函数的性质以及待定系数法求二次函数的解析式，得出顶点的坐标是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．
如图，直线AB∥CD，BC平分∠ABD，若∠1=65°，则∠2的大小为（ ）
如图，直线AB∥CD，BC平分∠ABD，若∠1=65°，则∠2的大小为（ ）| A． | 35° | B． | 40° | C． | 50° | D． | 65° |
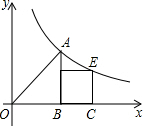在平面直角坐标系中，等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上，函数y=$\frac{k}{x}$（k＞0）的图象过点A，E．若BC=1，则k的值等于$\frac{3+\sqrt{5}}{2}$．
如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，连接DE交AC于点F．