题目内容
17．
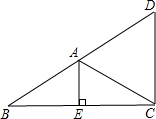已知：如图AE⊥BC，∠EAC=∠ACD，试说明BC垂直于DC．
分析 利用平行线的判定推出AE∥CD，再根据平行线的性质及垂线定义可得出．
解答 解：∵AE⊥BC，
∴∠AEB=90°，
∵∠EAC=∠ACD，
∴AE∥CD，
∴∠DCB=∠AEB=90°，
∴BC⊥DC．
点评 本题考查了平行线的判定和性质，垂直的定义，熟练掌握平行线的判定定理是解题的关键．
练习册系列答案
相关题目
7．
如图，直线AB∥CD，BC平分∠ABD，若∠1=65°，则∠2的大小为（ ）
如图，直线AB∥CD，BC平分∠ABD，若∠1=65°，则∠2的大小为（ ）| A． | 35° | B． | 40° | C． | 50° | D． | 65° |
如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，连接DE交AC于点F．
5．
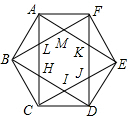如图，正六边形ABCDEF的边长为6，连接对角线AC，BD，CE，DF，EA，FB，这些对角线相交得到正六边形HUKML，则得到的正六边形HUKML的面积为（ ）
如图，正六边形ABCDEF的边长为6，连接对角线AC，BD，CE，DF，EA，FB，这些对角线相交得到正六边形HUKML，则得到的正六边形HUKML的面积为（ ）| A． | 18$\sqrt{3}$ | B． | 36$\sqrt{3}$ | C． | $\frac{9\sqrt{3}}{2}$ | D． | $\frac{18\sqrt{3}}{2}$ |
12．收音机刻度盘的波长和频率分别是用米（m）和千赫兹（kHz）为单位标刻，下面是它们的一些对应的数值：
根据表中波长（m）和频率（kHz）的对应关系，当波长为800m时，频率为375kHz．
| 波长（m） | 300 | 500 | 600 | 1000 | 1500 |
| 频率（kHz） | 1000 | 600 | 500 | 300 | 200 |
2．
如图，在平面直角坐标系中，⊙O的半径为2，AC，BD是⊙O的两条互相垂直的弦，垂足为M（1，$\sqrt{2}$），则四边形ABCD面积最大值为（ ）
如图，在平面直角坐标系中，⊙O的半径为2，AC，BD是⊙O的两条互相垂直的弦，垂足为M（1，$\sqrt{2}$），则四边形ABCD面积最大值为（ ）| A． | 2$\sqrt{6}$ | B． | 5 | C． | 4 | D． | 6 |
7．已知x+y=6，xy=4，则x2y+xy2的值为（ ）
| A． | 12 | B． | -12 | C． | -24 | D． | 24 |