题目内容
4.若(x+m)(x2-3x+n)的展开式中不含x2和x项,则m,n的值分别为( )| A. | m=3,n=1 | B. | m=3,n=-9 | C. | m=3,n=9 | D. | m=-3,n=9 |
分析 根据多项式与多项式的乘法法则展开后,将含x2与x的进行合并同类项,然后令其系数为0即可.
解答 解:原式=x3-3x2+nx+mx2-3mx+mn
=x3-3x2+mx2+nx-3mx+mn
=x3+(m-3)x2+(n-3m)x+mn
∵(x+m)(x2-3x+n)的展开式中不含x2和x项
∴m-3=0,n-3m=0
∴m=3,n=9
故选(C)
点评 本题考查多项式乘以多项式的运算法则,解题的关键是先将原式展开,然后将含x2与x的进行合并同类项,然后令其系数为0即可.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
19.在3.14,-$\sqrt{7}$,π,$\frac{1}{3}$,-0.23,1.131331333133331…(每两个1之间依次多一个3)中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.方程x2-2x=0的解为( )
| A. | x=2 | B. | x=0 | C. | x1=0 或 x2=2 | D. | x1=0 或 x2=-2 |
16. 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
 如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.
如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.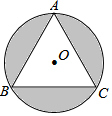 如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$. 有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )