题目内容
12.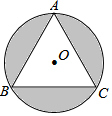 如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
分析 利用正三角形的性质,由它的内接圆半径可求出它的高和边,再用圆的面积减去三角形的面积即可.
解答 解:如图,点O既是它的外心也是其内心,
∴OB=2,∠1=30°,
∴OD=$\frac{1}{2}$OB=1,BD=$\sqrt{3}$,
∴AD=3,BC=2$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$×2$\sqrt{3}$×3=3$\sqrt{3}$;
而圆的面积=π×22=4π,
所以阴影部分的面积=4π-3$\sqrt{3}$,
故答案为4π-3$\sqrt{3}$.
点评 本题考查的是正多边形和圆、特殊角的三角函数值及三角形的面积、圆的面积公式等知识,熟练掌握正三角形的性质,特别是它的外心,内心,重心,垂心重合.记住正三角形的内切圆半径,外接圆半径和它的高的比(1:2:3)是解题的关键.

练习册系列答案
相关题目
7.已知$\frac{1}{p}$=$\frac{v}{m}$-2,且p≠-$\frac{1}{2}$,则m=( )
| A. | $\frac{pv}{1+2p}$ | B. | $\frac{pv}{1-2p}$ | C. | $\frac{pv}{2p-1}$ | D. | $\frac{v-2}{p}$ |
17.如果收入100元记作+100元,那么支出70元应记作( )
| A. | +70元 | B. | -170元 | C. | -70元 | D. | +170元 |
4.若(x+m)(x2-3x+n)的展开式中不含x2和x项,则m,n的值分别为( )
| A. | m=3,n=1 | B. | m=3,n=-9 | C. | m=3,n=9 | D. | m=-3,n=9 |
1. 如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )
如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )
 如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )
如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )| A. | x<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<x<1 | C. | x<1 | D. | -1<x<1 |
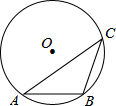 如图,⊙O中,点C是优弧ACB上一点(不与A、B重合),cosC=$\frac{4}{5}$,弦AB=6,则半径r=5.
如图,⊙O中,点C是优弧ACB上一点(不与A、B重合),cosC=$\frac{4}{5}$,弦AB=6,则半径r=5.